Previous Month | RSS/XML | Current | Next Month

WEBLOG

February 29th, 2016 (Permalink)

The Puzzle of the Sleeper Cells

The Agency for Counter-Terrorism (ACT) has discovered the existence in a target country of a sleeper cell of agents of a foreign power, though I cannot here reveal the names of either the target country or the foreign power. In addition to discovering the cell, the ACT recovered a secret document outlining the strict rules used by this power in its sleeper cell operations in target countries. There are two security rules, that is, rules designed to protect the whole sleeper cell operation:

  1. "The egg basket rule": This is the rule that never are all the sleeper agents in a country to be part of the same cell.
  2. "The triad rule": Every sleeper cell consists of three and only three sleepers.

In addition, there are rules designed to make it possible for separate cells to communicate with one another, which is facilitated by the fact that individual sleepers may belong to more than one cell. There are two inflexible rules of communication:

  1. "The monogamy rule": Any two sleeper agents in the same country are in one and only one cell together.
  2. "The overlap rule": Any two cells have one, but only one, sleeper in common.

These rules are rigidly adhered to, and the foreign power would shut down its entire sleeper operation rather than violate a rule. Of course, what ACT would most like to know is just how many sleeper agents they should look for. Can you help? Can you determine from the above information what is the minimum number of sleeper agents there are in the target country?

Solution

February 23rd, 2016 (Permalink)

Movie Review: Best of Enemies

I've reviewed books here previously, but this is the first movie review―and maybe the last! Best of Enemies is a documentary film that, after a theatrical run last year in a small number of theaters, is now available on DVD and streaming. The movie is relevant to this election year because it is built around a little-known event that took place in 1968, which was also an election year.

The event in question happened during a series of televised "debates" between conservative columnist William F. Buckley, Jr. and leftist writer Gore Vidal that were shown during the ABC TV network's coverage of the political conventions. Much of the movie is taken up with stage-setting the incident for younger viewers who are probably not familiar with its protagonist and antagonist, or the political state of the union in that tumultuous year. The two "debaters" are both dead, and probably no longer well-known to many.

At the risk of spoiling it for those who have not seen it, the climax of the movie is built around an exchange during one of the debates of less than a minute. Vidal first insinuates that Buckley is a "crypto-Nazi", then Buckley calls Vidal a "queer" and threatens to punch him in the face if he repeats the insinuation.

This language is not likely to shock most younger viewers who are used to far worse on television than was allowed in 1968. Moreover, this is an election year when just this month one presidential candidate has called another a "pussy", and the same candidate said that he would like to punch a disruptive protester in the face―see the Sources, below, if you don't believe me. In comparison, the Buckley-Vidal exchange may seem anti-climactic. There is a threat of violence, but no actual violence. Oh, for the good old days, when it was the pundits and not the candidates who insulted and threatened each other!

1968 was not only an election year, but the year that Robert F. Kennedy and Martin Luther King, Jr. were both assassinated. The Vietnam War was at or near its height, with the Tet offensive occurring at the beginning of the year. There was also rioting following King's assassination, and during the Democratic convention during which the confrontation between Buckley and Vidal occurred. So, the name-calling and threats of the debate can be seen as a microcosm of the tension and violence in the streets.

The movie tries to make this minor brouhaha seem more important than it was―in fact, important enough to make a movie about―by suggesting that it was the first incident of screaming heads on TV. I'm unsure whether it was the first, but even if it was why is that so important? There's always a first time.

However, there's little evidence given in the movie that the contretemps had any lasting effect. Of course, it's true that subsequent TV political "debates" have become louder and more vicious in the years since, but that doesn't mean that this one caused such a decline in civility. If so, it had a rather delayed reaction, since nothing much changed until the '80s. CNN's Crossfire show, which was much maligned by Jon Stewart for its partisan and sometimes combative tone, didn't begin until early in that decade. Morton Downey Jr.'s infamously raucous talk show premiered in 1987, while Geraldo Rivera had his nose broken during a brawl on his show in 1988.

The movie claims that the ratings of ABC's convention coverage were good enough to influence these later developments, but the central incident didn't occur until the penultimate debate of the second of the two conventions. So, it seems unlikely that it had much to do with any good ratings ABC may have enjoyed. I suppose that it's possible that a lot of people who missed the fighting words tuned in the next night in the hopes of seeing a fist fight, but if so they were disappointed.

Buckley and Vidal never appeared on a debate show together again, though that was probably mostly due to the antipathy between the two. By the time of his dust-up with Vidal, Buckley had already started his long-running show Firing Line, which was a model of sedate―even boring―decorum. Vidal made some subsequent appearances on talk shows―including an episode of Playboy After Dark, as the movie shows!―but, as far as I know, was never a regular.

Even more telling is the fact that ABC doesn't appear to have continued the debate format in its coverage of the 1972 conventions―at least, the movie doesn't mention any such thing. However, if there were such debates in subsequent convention coverage, they appear to have been more civil, because if they hadn't been I'm sure the movie would have mentioned it. So, the movie simply doesn't make a good case for the baneful influence of the spat between Buckley and Vidal.

The movie does successfully put the near-fight in some context. The extent to which most people are familiar today with it is probably from short clips on YouTube, whereas the movie shows that Vidal had been needling Buckley from the very first debate. Moreover, it appears that Vidal had an intentional strategy to cause Buckley to lose his temper, which is an old debater's trick. Of course, Vidal's ad hominems in no way excuse Buckley's ad baculum even if they make it more emotionally understandable.

While I don't buy the notion that the kerfuffle between Buckley and Vidal is of great historical importance, it could serve as an example of what is wrong with so much of our current political debate. In Best of Enemies, the story of a series of debates becomes the history of the enmity between two men, together with the surrounding circumstances that led to their confrontation, as well as its repercussions on their lives. The political issues that Buckley and Vidal were supposed to be debating during those conventions are lost in this personal story, just as so much of our current "debates" are about personality, not politics.

If anything approaching the Buckley-Vidal tiff were to occur in one of the current season's "debates" between presidential candidates, it would top the news the next day and be the main topic of conversation. Almost everyone in the country would hear about it and see short clips of the exchange, just as most people who have heard of the clash between Buckley and Vidal have only seen a brief clip of it. Despite its failure to make a case for their earth-shattering importance, I'm interested in the debates, and my greatest disappointment is how little of them you see. Few in today's audience know anything about the controversies of the political conventions of that year, and perhaps fewer care. But if you remove all that, what's left? Just two now-dead guys insulting and threatening each other. Best of Enemies isn't an exposé of what's wrong with political argumentation today; it's an example of it. It exploits the very subject it is supposedly exposing.

So what, if anything, can we learn from Best of Enemies that applies to our current political debates? For the reasons above, I don't think there's much to be learned from the movie itself, but it does draw our attention to a famous episode of incivility in debate, and perhaps it's a good opportunity to review why civility is an important value.

First of all, the debate in '68 was not, or should not have been, about either William F. Buckley, Jr. or Gore Vidal, since neither man was running for office. Personalizing the debate took attention away from the serious issues that were causing the rioting in the streets outside, and it was those issues that should have been the focus.

Secondly, it's difficult for debaters to find common ground or to settle disputes that are polluted with insults and threats. Buckley and Vidal never debated again because of the personal enmity that was a consequence of this incident. Instead, as the movie briefly mentions, they took each other to court. In previous centuries, they might have met in a field for a duel. Debate is supposed to be a rational and civilized alternative to violence, rather than an incitement to it.

Sources:

February 16th, 2016 (Permalink)

Humpty-Dumptying

"…There's glory for you!" [said Humpty Dumpty.]

"I don't know what you mean by 'glory,'" Alice said.

Humpty Dumpty smiled contemptuously. "Of course you don't―till I tell you. I meant 'there's a nice knock-down argument for you!'"

"But 'glory' doesn't mean 'a nice knock-down argument,'" Alice objected.

"When I use a word," Humpty Dumpty said in rather a scornful tone, "it means just what I choose it to mean―neither more nor less." …

Alice was too much puzzled to say anything, so after a minute Humpty Dumpty began again. "…Impenetrability! That's what I say!"

"Would you tell me, please," said Alice "what that means?"

"Now you talk like a reasonable child," said Humpty Dumpty, looking very much pleased. "I meant by 'impenetrability' that we've had enough of that subject, and it would be just as well if you'd mention what you mean to do next, as I suppose you don't mean to stop here all the rest of your life."

"That's a great deal to make one word mean," Alice said in a thoughtful tone.
Source: Lewis Carroll, "Chapter 6: Humpty Dumpty", Through the Looking Glass

Another "debate" was held a few days ago between the Democratic candidates. These so-called debates are happening so frequently that I can't keep up, and I don't know which number this was. The race on the Democratic side is now down to two candidates: former Secretary of State Hillary Clinton and Senator Bernie Sanders. In answer to a question about the size of government from moderator Judy Woodruff, Sanders answered in part:

…[In the United States] today you have massive levels of income and wealth inequality, when the middle class is disappearing, you have the highest rate of child poverty of almost any major country on Earth. …[I]n my view, the government of a democratic society has a moral responsibility to play a vital role in making sure all of our people have a decent standard of living.
Source: Team Fix, "Transcript: The Democratic debate in Milwaukee, annotated", The Washington Post, 2/11/2016

The operative part here is the highlighted claim, though I've included some context to clarify it. Notice, first, that it's carefully hedged: not "any" major country, but "almost any". Also, what's a "major" country and how many are there? Even so, it's still a shocking claim; but is it true? As we will see, it is in a sense, but we must first take a trip through the looking-glass to see in what sense.

Sanders has been making a version of this claim at least since last year, but then he wasn't hedging the "any" and Politifact rated the statement as "Mostly False"―see Source 2, below. Since then Sanders has added the "almost" and Politifact now rates it as "Half True", so I guess that's progress―see Source 3, below. Maybe if Sanders changes "almost any" to "most" Politifact will rate it "Mostly True".

I wish Politifact would stop arbitrarily carving up truth and falsity like a pie. Sanders' original claim was completely false, not mostly so. The current, hedged claim is entirely true―given what he appears to mean by it, as we shall see below―not half so.

Rather, the real problem with Sanders' statement is not with its truth-value, but that it simply does not mean what a typical speaker of the English language would understand it to mean. So, even though the current statement is technically true, it's still misleading. This is because Sanders uses two words in a Humpty Dumpty-like way:

  1. "Major": One might think that being a "major" country is a matter of size, either in area or in population, so that Russia and China would be "major" countries, and small countries such as Israel and Iceland would be "minor" ones. However, according to Sanders' spokespeople, by "major" countries Sanders means members of the international Organisation for Economic Cooperation and Development (OECD). Russia and China are not members of OECD, and thus neither is a "major" country, according to Sanders' idiolect, while member countries Israel and Iceland are.
  2. "Poverty": What most English speakers understand by "poverty" is what's also called "absolute poverty", which is falling below what Sanders calls "a decent standard of living". However, there is also "relative poverty", which simply means being "poor" relative to someone else, that is, having less money than some others have. Of course, almost everybody has less money than Bill Gates, and even Bill Gates has less than some, so almost everyone is relatively poor. Since such a wide concept would have little use, those who want to measure "relative poverty" have to define it in some specific way.

    There are two technical definitions of "relative poverty" in the studies that Sanders based his changing claims on, both of which define it in terms of having an income less than a certain percentage of the median income in a country: either 50% or 60%. So, whether a given person in a particular country is relatively poor will depend on both the percentage selected and the median income of the country. As a result, it's perfectly possible for someone who lives in a wealthy country that has a high median income to be both relatively poor, by one of these definitions, but not absolutely poor.

    There's nothing inherently wrong with such a technical definition, but it does not measure what most people think of as poverty, namely, lacking "a decent standard of living". Instead, it measures the amount of income inequality in a country, that is, the greater the range of incomes, the more people will fall below 50% or 60% of the median.

    If this point isn't obvious, consider the following example: Suppose that we have a small society of five families with the following incomes (in thousands of dollars): 10, 15, 20, 40, and 45. The median income in this little society is 20K. Using the 50% of median definition of poverty, there is one poor family in our society, namely, the one getting by on 10K. Now, suppose that a "rich" family that makes 50K a year moves to our miniature society: the median now increases to 30K―which is the mean of 20K and 40K, the two central values. As a result, the society now has two poor families, since the family making 15K is now at 50% of the median income. Yet, absolute poverty has not changed in this slightly larger society, since all of the original families are still making the same amount of money. All that has happened is that the arrival of a family that is richer than the others has increased relative poverty.

    A further problem with the notion of "relative poverty" is that, since it is really another name for income inequality, the only way to eliminate it would be to eliminate inequality, that is, everyone would have to make the same income. Otherwise, there will always be some who are poor relative to others. Suppose that, in the example above, the families were making millions of dollars, not thousands. Most people would not consider a family with an income of ten million dollars a year to be poor, yet it is relatively poor compared to the other members of this rich society. As the Bible almost says: "The relatively poor will always be with you."

Now, there's no logical objection to Bernie Sanders making a political issue out of income inequality in his campaign for president, and he has done so, but income inequality is not the same thing as poverty. Translated from Sanders' Humpty Dumpty language into English, his claim is that the U.S. has greater income inequality than almost all of the other members of the OECD.

It's a little unfair to compare Sanders to Humpty Dumpty since it's always obvious when the latter gives a word an unusual meaning. When he suddenly blurts out "glory" or "impenetrability", Alice can tell that she doesn't know what he means and ask for a definition. Sanders, in contrast, uses familiar words such as "major" and "poverty" in technical ways without the least warning. We would have no way to know what he meant if Politifact had not contacted his campaign to find out what justification there was for his shocking claim about poverty in major countries.

Sources:

  1. "List of OECD Member countries―Ratification of the Convention on the OECD", Organisation for Economic Cooperation and Development. Accessed: 2/12/2016.
  2. Christian Belanger, "Sanders: Child poverty is higher in America than any other major country", Politifact, 7/8/2015.
  3. C. Eugene Emery Jr., "Reports' limitations plague Bernie Sanders' claim about high childhood poverty rates in the U.S.", Politifact, 2/12/2016.
  4. Nigel Warburton, "Humptydumptying", in Thinking from A to Z (2nd edition) (2001).
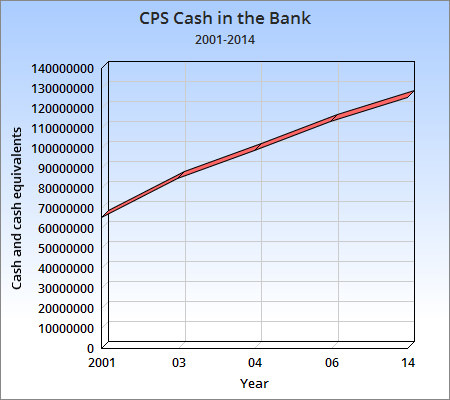
CPS Cash in the Bank
February 8th, 2016 (Permalink)

How to Grind Axes

Here's something I haven't seen before. Can you spot what's wrong with the chart shown? It doesn't fit any of the types of misleading graph I discussed here a few years ago, and I couldn't find any mention of this form of charting abuse in any of my usual sources.

The problem is with the x-axis and how it's labelled. A casual glance at the graph seems to show a steady rise in the "cash in the bank" over the years 2001 to 2014. However, a closer look reveals that the first quarter covers the two years from 2001 to 2003, the second quarter represents only one year, the third quarter is again two years, but the last covers eight years! As a result, the first three-fourths of the x-axis represents six years, while the last fourth covers eight. 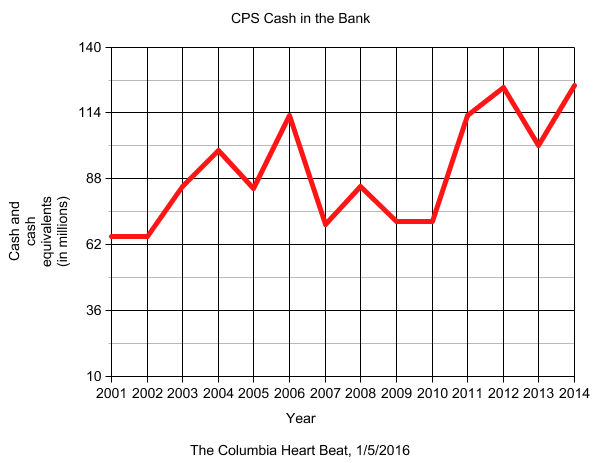CPS Cash in the Bank

A further aspect of this graph is that only the data for the specific years listed on the scale are charted, whereas data for every year covered was available―see the Source, below. To the right, I include a graph that shows the data for every year. Clearly, the rise in cash over the fourteen year period was much less smooth than the original graph shows. Notice, especially, that the last quarter of the old graph occupies about two-thirds of the new one, from 2006 to 2014. While there was a slight increase during those years, it was a very bumpy ride, and the amount of cash on hand was actually down for the five years from 2006 to 2011.

It may be an unwritten rule that, unless you're using a logarithmic scale, the segments of the axes should represent equal amounts of the quantities represented. I don't recall ever seeing this convention stated explicitly, but neither do I remember ever seeing a chart which broke it. I expect that most readers of graphs will assume that this rule is followed, and may not pay close attention to the labels on the scales that indicate otherwise. Once you start manipulating the axes in this way, almost any misrepresentation would be possible, and many readers are likely to get a false impression.

Source: Heart Beat Staff, "UP! Even CoMo's tax lovers astonished by school district tax hike", The Columbia Heart Beat, 1/5/2016

Via: Kaiser Fung, "How to print cash, graphically", Junk Charts, 1/27/2016

February 3rd, 2016 (Permalink)

New Book: Republic of Spin

Instead of trying somehow to banish spin from the kingdom of politics, we'd be better off…trying to inculcate a critical sense that helps us question and evaluate spin―and maybe, just once in a while, to know when to believe it.
Source: David Greenberg, Republic of Spin, p. 10

Since this is a year in which we elect a new president, what could be more timely than presidential historian David Greenberg's new book Republic of Spin: An Inside History of the American Presidency? I haven't read it yet, of course, but judging from the table of contents the book covers the history of presidential spin from Teddy Roosevelt up to the present day. The book's focus seems to be on the spin that emanates from the White House after a politician is elected to the presidency, as opposed to the sort that will be making us dizzy over the next nine months. Nonetheless, the techniques of spin in the two situations are much the same, so this book sounds promising.

Source: Michael Beschloss, "David Greenberg’s ‘Republic of Spin’", The New York Times, 1/20/2016. A favorable review from a fellow presidential historian.

Solution to the Puzzle of the Sleeper Cells: There are at least seven sleeper agents.

Here's one way to figure this out: We know from the ACT that there is at least one sleeper cell in the target country. We also know, from the triad rule, that there are three sleeper agents in every cell. So, there are at least three sleepers in the country, but is that the minimum? Let's call these sleepers "A", "B", and "C" and the cell that they are in "ABC". Moreover, the egg basket rule tells us that these three cannot be the only sleepers in the target country, so there must be at least one additional sleeper: let's call this one "D".

Now, D cannot be in cell ABC, since it's fully occupied. However, according to the monogamy rule, D must be in a cell with each of A, B, and C. Moreover, D cannot be in a single cell with more than one of these three sleepers, because of the monogamy rule, again. To see this, suppose that A, B, and D were in a cell together; but A and B are already in the cell ABC together, which would mean that there are two distinct cells with both A and B in them, which is ruled out by the monogamy rule. Similar reasoning applies to grouping A, C, and D, or B, C and D together. Therefore, there must be three distinct cells, one containing A and D, another with B and D, and a third with C and D.

Now, the triad rule tells us that each of these three cells containing D must have three sleepers, so there must be three additional sleepers distinct from A, B, C, and D―let's call them "E", "F", and "G"―which make up the three cells: ADE, BDF, and CDG. There are three additional cells required by the four rules: BEG, CEF, and AFG.

We have now established that there are at least seven sleeper agents. For extra credit, determine the maximum number of sleepers in the target country.

Extra Credit: This is harder to prove, which is why it gets extra credit. So, if you couldn't figure it out, don't feel too bad! On the other hand, if you did figure it out, feel very good!

We can show that there are at most seven sleepers by a reductio ad absurdum argument: Suppose that there were an eighth sleeper; let's call him or her "H". By the monogamy rule, there would have to be a cell that both A and H are in together. Now, consider the cell BDF, whose existence we established in the previous section: by the overlap rule, these two cells would have to share a common member. However, that common member cannot be B, since A and B are already in the cell ABC together, and monogamy rules out that they are in two distinct cells. Similar considerations apply to both D and F, since A and D are already in ADE together, and A and F are in the cell AFG. Thus, if there were an eighth sleeper agent, either the monogamy or the overlap rule would be violated. Hence, there is no eighth agent.

Therefore, we have shown that there are at least seven, and at most seven sleepers, which means that there are exactly seven sleeper agents.

Sources:

Previous Month | RSS/XML | Current | Next Month