Previous Month | RSS/XML | Current | Next Month
August 29th, 2016 (Permalink)
Don't Check it Out, Too
I have a book review of Scrutinizing Argumentation in Practice, edited by Frans van Eemeren and Bart Garssen, in the latest issue of the journal Cogency. The book is a collection of scholarly conference papers, so probably not of interest to the casual or beginning student of argumentation. However, if you're interested in taking a deeper dive into the topic, do check it out.
Source: Gary N. Curtis, "Review of Scrutinizing Argumentation in Practice", Cogency, Vol. 8, No. 1 (111-121), Winter 2016
August 24th, 2016 (Permalink)
Don't Check it Out
Brian "Skeptoid" Dunning has a new podcast about the meme that says you shouldn't criticize something unless you've tried it. The title for this entry doesn't refer to the podcast: Do check it out!
The meme is quite obviously not generally good advice: I've never jumped out of an airplane without a parachute, but I'm rather critical of the idea. I'm sure that the first few seconds are thrilling; it's what comes after that concerns me.
I generally agree with Dunning, but would like to add my own take on this, relating the issue more explicitly to the three logical fallacies that Dunning alludes to:
- Post Hoc: The sort of things that people keep telling Dunning to shut up about unless he's tried them are "alternative" medical treatments and the like. The trouble with evaluating such treatments by trying them is that most medical problems will eventually improve on their own, so if you try some new "treatment" you may well improve for reasons having nothing to do with the treatment.
The post hoc effect can even go the opposite direction: I recently began a course of treatment with a daily medication that I had never taken before. Shortly after beginning the new treatment, I experienced extreme back pain. This led me to wonder whether the pain was caused by the medication, though this was not a known side effect. Fortunately, the pain went away after a few hours and was probably due to raking the yard rather than the new medication. However, the coincidence of the pain occurring so soon after starting the medicine was compelling enough to cause me to temporarily stop taking it.
One thing that Dunning says that I disagree with is the following: "Crediting something with efficacy because it appeared to work when you tried it is a perfectly rational conclusion for an intelligent person to make." If you substituted the word "normal" for "rational", I would agree. It's normal for people to think that way, just as I did when I hurt my back, but it ain't rational. That's why the post hoc fallacy is such a common one. Moreover, it's often just plain impossible for us to tell what caused what, especially when you're talking about health. Viruses and bacteria are too small to see, and you generally can't see inside your own body to tell what's going on in there. That's what you need science for.
- Hasty Generalization: You're only one data point. Even if you have experienced something, you shouldn't generalize from the experience of just one person, even if that person is you―that's as hasty a generalization as you can get. Just because something "worked" for you doesn't mean that it will "work" for anyone else, so you shouldn't generalize to other people. Not only that, but just because something worked in the past doesn't mean that it will work in the future, so you shouldn't even generalize for your future self on the basis of just one past experience.
- The Anecdotal Fallacy: The anecdotal fallacy is the tendency for a vivid anecdote―or story―to overwhelm other and better evidence, and what could be more vivid than your own experience?
Source: Brian Dunning, "Don't Try It Before You Knock It", Skeptoid, 8/23/2016
August 17th, 2016 (Permalink)
Lesson in Logic 13: Categorical Statements
A categorical statement is one that asserts something about a category, that is, a class or type of thing. Classes are talked about using class terms, which are common nouns or noun phrases.
Examples of class terms: "shoes", "ships", "cabbages", "kings", "pileated woodpeckers"
As mentioned in lesson 11―see the Previous Lessons, below―classes need not have members, and some class terms refer to such empty classes.
Examples of empty class terms: "unicorns", "vampires", "werewolves", "passenger pigeons"
Moreover, there also terms for classes about which we may not know whether they are empty or not.
Examples: "bigfeet", "Loch Ness monsters", "ivory-billed woodpeckers"
The simplest categorical statements are those that talk about a single class, and thus contain a single class term. The simplest thing that you can say about a single class is that it is non-empty or empty, that is, that something of that type exists or does not exist. You learned in a previous lesson how to represent on a class diagram that a single class is empty or non-empty by using shading to represent emptiness and an "X" to represent a non-empty class.
The type of categorical statements that you will learn about in this lesson contain two class terms, but representing them on a two-circle Venn diagram is a simple extension of what you've already learned. There are four types of such statements that are studied in traditional logic and designated by the letters: A, E, I, and O. The I and O type of statement say something about "some" member of the subject class, so an "X" is used to indicate that a subclass is non-empty.

I: An I statement has the form: "Some A is a B".
Example: Some arguments are syllogisms.
There are many ways to express I statements in English, including: "some As are Bs", "there are As that are Bs", etc. This type of statement relates two classes by asserting that at least one member of the first class, A, is also a member of the second class, B. To use a Venn diagram to represent this information you need to show that there is something in A that is also in B, that is, that something is in the overlap of the two classes.
The A and E types of statement assert that a certain subclass is empty, so you will need to use shading instead of an "X".
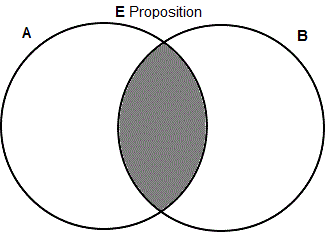
E: An E statement has the form: "No A is a B".
Example: No bats are birds.
There are many ways to express E statements in English, such as "no As are Bs", as in the Example. This type of statement relates two classes by asserting that no member of the first class, A, is a member of the second class, B. E statements are the opposite of I statements in that the I asserts that there is something in the overlap of the two classes, whereas the E asserts that there is nothing there. Thus, to represent this information on a Venn diagram we need to show that there is nothing in A that is in B, that is, that the overlap area is empty. So, instead of an "X", you shade in the overlap as shown.
Exercises: If you understand how to represent the I and E statements on Venn diagrams, you should be able to figure out how to represent the other two traditional categorical statements. For the following two exercises, draw the primary diagram and label the circles "A" and "B", then use either an "X" or shading to indicate that a subclass in the diagram is either non-empty or empty:
- "Some A is not a B."
- "All As are Bs."
In the next lesson, you'll learn how to use these diagrams to determine logical relationships between these four types of categorical statement.
Previous Lessons:
- Lesson in Logic 11: Class Diagrams, 6/22/2016
- Lesson in Logic 12: Two-Circle Venn Diagrams, 7/16/2016
August 12th, 2016 (Permalink)
You May Need a Napkin
Check out this quote from the beginning of a New York Times editorial:
Global trade allows Americans to satisfy their appetites for strawberries in spring, apples in midsummer and asparagus in autumn. … But getting fresh produce year round also means that consumers are exposed to foreign food production systems that may not be well regulated. Although the vast majority of the 30 billion tons of food imported annually is wholesome, recent incidents of illness caused by tainted Guatemalan raspberries…have made food safety a public concern.
Source: "Safety Standards for Imported Food", International New York Times, 10/3/1997
Is there anything there that grabs your attention? Something that makes you feel a bit doubtful―a little skeptical? No?
How about the claim that "30 billion tons of food [is] imported annually". If you're like me, you have no idea how much food is imported into the United States on a yearly basis. In fact, you may have no notion of even a ballpark figure; is it millions or billions of tons? Do you have a sense of how much food a ton is? I wouldn't blame you if you just read over that claim with glazed eyes and didn't think about it at all. You probably would just accept it because it is the Times, after all, and surely they know what they're talking about.
Don't do that, because this is a claim that you can easily test yourself. I'm not talking about doing research on how much food is imported annually. No, I'm talking about doing a simple back-of-the-envelope calculation (BOTEC) to test the claim for sanity. Such calculations are called "back-of-the-envelope" because they are short and simple enough to be scribbled on an envelope or even a cocktail napkin.
How do you do such a test? Here's a hint: use elementary math together with what you already know―that's all you'll need. Try to transform a number that is too big to grasp into one that you can evaluate using common sense.
Give it a try, then click on the link below when you think you've figured it out.
Go to the Back of the Envelope
August 11th, 2016 (Permalink)
New Book: A Survival Guide to the Misinformation Age
I haven't read the new book with the above title, so this is not an endorsement―just a notice. The author is David J. Helfand, an astronomer, which presumably explains its subtitle: Scientific Habits of Mind. I could certainly use a survival guide to misinformation, and this one appears promising. Judging from the chapter titles, the book has sections on the following topics:
- Logic and Language: Interlude 2
- Charts & Graphs: Chapter 5
- Lies, Damn Lies, and Statistics: Ch. 7
- Correlation ≠ Causation: Ch. 8
I'm especially excited to see a chapter on back-of-the-envelope calculations (BOTECs) (ch. 4), since I've complained for years that they are an important skill that books and courses on logic and critical thinking fail to teach. Some of the misinformation that inundates us every day can be debunked with a BOTEC, so that one doesn't need to do any research to show that it can't be true. This book may be worth getting for that chapter alone.
August 6th, 2016 (Permalink)
The Second Puzzle of the Sleeper Cells
The Agency for Counter-Terrorism (ACT) has again discovered the existence in a target country of a sleeper cell of agents of a second foreign power―see the Previous Puzzle, below, for the first case. Once again, I cannot here reveal the names of either the target country or the foreign power. In addition to discovering the cell, the ACT recovered a secret document outlining the strict rules used by this power in its sleeper cell operations in target countries. According to the secret document, this second power did not use the set of four rules that the first power used. Instead, it used the following two rules:
- "The membership rule": Every sleeper agent belongs to exactly two cells.
- "The overlap rule": Any two cells have exactly one sleeper in common.
These rules are rigidly adhered to, and the foreign power would shut down its entire sleeper operation rather than violate a rule. In addition, the secret document reveals that the power currently has exactly five cells in the target country. Of course, what ACT would most like to know is just how many sleeper agents they should look for. Can you help? Can you determine from the above information what is the exact number of sleeper agents there are in the target country?
Previous Puzzle: The Puzzle of the Sleeper Cells, 2/29/2016
August 1st, 2016 (Permalink)
Headline
McDonald’s Nixing Some Unpalatable Ingredients
Only "some"? That could explain a lot.
The Back of the Envelope: I mentioned that our new book this month has a chapter on BOTECs, and this excellent example comes from that chapter―see the previous weblog entry. Note that the following BOTEC is just one way to tackle this sanity check. So, if you went about it a different way, that's fine, but you should come up with a similar result.
As mentioned previously, one way to check a large number for sanity is to reduce it to a smaller number that you can test against your personal experience. In this case, you probably lack personal experience with the amount of food imported into the U.S. each year, but you do have some sense of how much you eat. So, let's figure out what your share of the imported food amounts to: to do this, you need to know only one additional fact, and that is the approximate population of the U.S. The current population of the U.S. is over 300 million people, but the article is from almost twenty years ago. Let's take 300 million as the approximate population of the U.S. in 1997―we don't need an exact figure anyway, since what we're doing is a rough estimate, and 300 million is a nice, round figure that divides into 30 billion easily.
30 billion tons divided among 300 million people is 100 tons of imported food per person per year, so that's your share. Now, a hundred tons sounds like an awful lot, but you probably still don't have a good sense of how much food that is. Since it's for a year, let's continue by dividing the amount into a daily figure; in other words, divide 100 tons by 365. To do this, it helps to know that a ton is 2,000 pounds, so that a hundred tons is 200,000 pounds, since it's easier to divide 365 into 200,000 than into 100; also, an answer in pounds will be easier to understand than one in a fraction of a ton. The result is approximately 548 pounds a day.
Do you eat 548 pounds of imported food a day? Remember, that's just imported food; surely you eat as much or more food grown in the U.S., assuming that you live here. So, for this claim to be true, you would have to eat over a thousand pounds of food a day. No wonder there's an obesity crisis in the U.S.!
Joking aside, the original claim is clearly insane, since it's too large by three orders of magnitude. Since three orders of magnitude is a factor of a thousand, and the difference between a million and a billion is a factor of a thousand, it's likely that the claim in the article is the result of a typo. In other words, the amount of food imported annually was probably 30 million, rather than billion, tons.
In any case, one lesson of this example is: don't believe everything you read, not even in The New York Times!
Source: David J. Helfand, A Survival Guide to the Misinformation Age: Scientific Habits of Mind (2016), p. 60
Solution to the Second Puzzle of the Sleeper Cells: There are ten sleeper agents.
According to the secret document, there are five sleeper cells, so let's call these cells 1 through 5. By the overlap rule, each cell must have exactly one agent in common with the other four cells. Since no agent can be in more than two cells, by the membership rule, this means that there are at least four distinct agents in each cell. In the case of cell 1, let's call these four agents A through D.
That there are exactly four such agents in each cell can be seen in the following way: suppose that there were an agent X in cell 1, distinct from agents A through D. By the membership rule, X would have to be in one of the other cells, but this would mean that cell 1 would share more than one agent with one of the other cells, violating the overlap rule. Thus, there is no agent X.
Since we know that there are five cells with four agents apiece, let's make out a chart showing what we know so far:
| Cells | Agent 1 | Agent 2 | Agent 3 | Agent 4 |
|---|---|---|---|---|
| 1 | A | B | C | D |
| 2 | A | |||
| 3 | B | |||
| 4 | C | |||
| 5 | D |
Now, let's start filling in the rest of the sleeper cells. Cell 2 must have three agents distinct from agent A, who is shared with cell 1. Let's call them E, F, and G:
| Cells | Agent 1 | Agent 2 | Agent 3 | Agent 4 |
|---|---|---|---|---|
| 1 | A | B | C | D |
| 2 | A | E | F | G |
| 3 | B | |||
| 4 | C | |||
| 5 | D |
By the overlap rule, cell 2 must share a distinct agent with each of the other cells. It already shares agent A with cell 1, so let's fill in the others:
| Cells | Agent 1 | Agent 2 | Agent 3 | Agent 4 |
|---|---|---|---|---|
| 1 | A | B | C | D |
| 2 | A | E | F | G |
| 3 | B | E | ||
| 4 | C | F | ||
| 5 | D | G |
Again, cell 3 must have two agents distinct from agents B and E, who are shared with cells 1 and 2, respectively. Let's call these two agents H and I:
| Cells | Agent 1 | Agent 2 | Agent 3 | Agent 4 |
|---|---|---|---|---|
| 1 | A | B | C | D |
| 2 | A | E | F | G |
| 3 | B | E | H | I |
| 4 | C | F | ||
| 5 | D | G |
Again, by the overlap rule, cell 3 must share a distinct agent with each of the other cells. It already shares agent B with cell 1 and E with cell 2, so let's fill in the others:
| Cells | Agent 1 | Agent 2 | Agent 3 | Agent 4 |
|---|---|---|---|---|
| 1 | A | B | C | D |
| 2 | A | E | F | G |
| 3 | B | E | H | I |
| 4 | C | F | H | |
| 5 | D | G | I |
We're almost done! All that's left is to add an additional agent, J, to cell 4, and J must also be shared with cell 5:
| Cells | Agent 1 | Agent 2 | Agent 3 | Agent 4 |
|---|---|---|---|---|
| 1 | A | B | C | D |
| 2 | A | E | F | G |
| 3 | B | E | H | I |
| 4 | C | F | H | J |
| 5 | D | G | I | J |
All of the cells are now filled and both of the rules have been followed, giving a total of ten agents, A through J.
Source: Jaime & Lea Poniachik, Hard-to-Solve Brainteasers (1998). The puzzle above was suggested by puzzle 38 on pages 24 and 75.
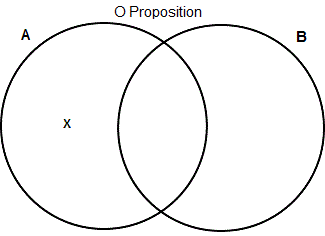
- O: An O statement has the form: "Some A is not a B".
Example: Some arguments are not syllogisms.
There are many ways to express O statements in English, including: "some As are not Bs" as in the Example, "there are As that are not Bs", "some As are non-Bs", etc. This type of statement relates two classes by asserting that at least one member of the first class, A, is not a member of the second class, B. Thus, to represent this information on a Venn diagram we need to show that there is something in A that is not in B, that is, that something is in the crescent-shaped area of A outside of the B circle.
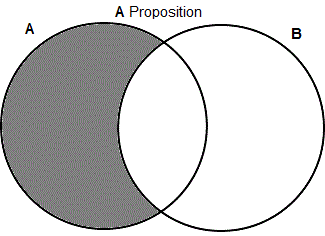
- A: An A statement has the form: "All As are Bs".
Example: All bats are mammals.
There are many ways to express A statements in English, including: "every A is a B", "any A is a B", "each A is a B", etc. This type of statement is trickier than the three previous types as it relates two classes by asserting that any member of the first class, A, is also a member of the second class, B. Thus, to represent this information on a Venn diagram we need to show that there is nothing in A that is not also in B, that is, that the crescent-shaped area in A is empty. You might well think that you should also put an "X" in the overlap area of A and B, as in an I proposition, to indicate that there are As that are Bs. If you know for a fact that A is a non-empty class, then no harm will be done by doing so, but if it's possible that A is empty then doing so would be a mistake.