The Existential Fallacy
Alias: The Fallacy of Existential Assumption1
Taxonomy: Logical Fallacy > Formal Fallacy > Quantificational Fallacy > The Existential Fallacy2
Form:
Any argument whose conclusion implies that a class has at least one member, but whose premisses do not so imply. Usually, this involves arguing from a universal premiss or premisses to a particular conclusion.
| Example | Counter-Example |
|---|---|
| All trespassers will be prosecuted. | All unicorns are animals. |
| Therefore, some trespassers will be prosecuted. | Therefore, some animals are unicorns. |
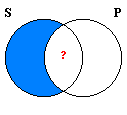
Venn Diagram:
This diagram represents both the Example and Counter-Example. The shading, which indicates the emptiness of a subclass, represents the truth of the premiss. The central overlap section would be nonempty if the conclusion were true, but the question mark indicates that it would be empty if the subject class as a whole is empty. Therefore, the diagram shows both arguments invalid since the premiss could be true while the conclusion is false.
Exposition:
A statement is said to have existential import3 if it implies that some class is not empty, that is, that there is at least one member of the class. For example:
| Existential Import | No Existential Import |
|---|---|
| There are black swans. | There are no ghosts. |
"There are black swans" implies that the class of black swans is not empty, whereas "There are no ghosts" implies that the class of ghosts is empty. To reason from premisses that lack existential import for a certain class to a conclusion that has it is to commit the Existential Fallacy.
History:
In the traditional formal logic of categorical syllogisms developed by Aristotle and subsequent logicians through the Middle Ages and up to the middle of the nineteenth century, it was assumed that the classes of things referred to by the subject and predicate terms of categorical propositions were non-empty. For this reason, certain arguments were considered valid that would not be valid if some class were empty: in particular, it was thought that an A-type proposition implied an I-type with the same subject and predicate terms, and an E-type implied an O-type, again with the same subject and predicate terms. This type of immediate inference was called "subalternation":
| All sapsuckers are woodpeckers. | No boobies are titmice. |
| Therefore, some sapsuckers are woodpeckers. | Therefore, some boobies are not titmice. |
Subalternation is validating if the subject class of the premiss is non-empty, but not otherwise. For reasons explained in the Exposure, below, logicians of the later nineteenth century dropped the traditional assumption of non-emptiness, and adopted what is called the "Boolean interpretation"―after logician George Boole5―of universal quantifiers. Under the Boolean interpretation, I- and O-type propositions have existential import―see the Exposition, above―whereas both A- and E-types lack it. This has the consequence that some immediate inferences―such as subalternation―and categorical syllogisms which were valid under the traditional interpretation become instances of the existential fallacy.
Exposure:
- A general principle of deductive reasoning is what I call "the no-free-lunch (NFL) principle", which is that you get in the conclusion what you pay for in the premisses. If you don't pay for something in the premisses, you don't get that something in the conclusion. A fancier way of putting this is that deduction is non-ampliative6, that is, the information contained in the conclusion does not go beyond that contained in the premisses. This is why in a valid deductive argument the premisses necessitate the conclusion: if the information contained in the premisses is true then the information contained in the conclusion must also be true, since the latter information is contained in the former. One correlary of the NFL principle is that in deduction you can't get something for nothing, which is why the existential fallacy is fallacious. To conclude that something exists you must assume in the premisses that it exists.
- People sometimes assume that if there is a meaningful term for a type of thing that type of thing must exist; even philosophers have been known to make this mistake. Of course, it's generally true that meaningful words stand for existing things, since the usual reason for creating a new word is to be able to refer to actual things. Nonetheless, there are exceptions, and we all know many words that refer only to imaginary or fictional objects, such as "vampire", "werewolf", "unicorn", and so on. Moreover, the traditional logic encouraged the notion that class names must have reference in order to be meaningful, thus supporting a kind of superstitious word magic according to which naming something brings it into existence.
The traditional theory makes it impossible to reason about empty classes, which might seem to be a small price to pay if all that we had to give up were classes such as unicorns. However, some classes may be empty for all we know, yet we manage to reason about them all the same. For instance, there may be no extraterrestrial aliens, but we cannot even say this meaningfully in the traditional theory, let alone use the class in an argument.
Also, consider a shopkeeper who puts up a sign saying: "All shoplifters will be prosecuted." The shopkeeper hopes that potential thieves will reason as follows: "According to the sign, if I shoplift, I'll be prosecuted. I don't want to be prosecuted. Therefore, I'd better not shoplift in this store." According to the traditional theory, if the sign succeeds in deterring shoplifters, then they cannot have reasoned in this way since there were no shoplifters to be prosecuted! Yet, it is partly because people reasoned in this way that there were no shoplifters.
- As long as the relevant classes are known to be non-empty, an argument that seems to commit the existential fallacy can be treated as an enthymeme with an implicit existential premiss―that is, a suppressed premiss asserting that there are things of a relevant type―instead of an instance of the fallacy. For instance, since there are both sapsuckers and boobies, the examples of Subalternation, above, are valid. Moreover, in a context in which people know about birds, it's unnecessary to mention the fact that there are birds of these types.
Notes:
- ↑ Irving M. Copi & Carl Cohen, Introduction to Logic (11th edition, 2001), p. 207.
- ↑ Madsen Pirie, How to Win Every Argument: The Use and Abuse of Logic (2013).
- ↑ Brian Duignan, "Existential Import", Encyclopaedia Britannica, accessed: 6/11/2025.
- ↑ Thanks to Todd Cruzen for pointing out problems with the previous examples of subalternation.
- ↑ "George Boole", Encyclopaedia Britannica, accessed: 6/11/2025.
- ↑ "Ampliative Argument", The Oxford Dictionary of Philosophy, accessed: 6/11/2025.
Revised: 6/11/2025