Previous Month | RSS/XML | Current | Next Month

WEBLOG

May 28th, 2015 (Permalink)

Cross-Check it Out

On October 28th, 2000, President Bill Clinton, in his weekly radio address made the following claims about the incidence of domestic violence against women in the United States:

Every 12 seconds another woman is beaten. That’s nearly 900,000 victims every year.
Source: "The President’s Radio Address", Government Printing Office, 10/28/2000 (PDF)

Are these numerical claims plausible? How could you go about checking them? Is there any way to do so without doing any research, that is, just using what you already know? When you've done your own plausibility check, click on "Check it Out", below, to see one way of checking these numbers.

Check it Out

Source: David Murray, Joel Schwartz & S. Robert Lichter, It Ain't Necessarily So: How Media Make and Unmake the Scientific Picture of Reality (2001), pp. xiii-xv.

May 26th, 2015 (Permalink)

Food is a Fallacy

Fads, I submit, are the very negation of reason. To be swept up in every new craze that comes along, to surrender oneself to idiocy just because everybody else is doing it―this to me, is the acme of mindlessness.
Source: Max Shulman, "Love is a Fallacy"

Slate had an article about a month ago, but which I just discovered, on the fallacious thinking behind food fads. Here's a taste:

Natural food is good. Evil foods harm you, but they are sinfully delicious, guilty pleasures. Good foods, on the other hand, are real and clean. … We’ve been primed to think this way. After all, the world’s most famous myth recounts a dietary fall from grace. Long ago, humans lived in an organic, all-natural, divinely designed garden, free from pesticides and GMOs and processed grains and sugar. But one day an evil advertiser came along and hissed, “Just eat this fruit.” Bam! Suddenly we were cursed with mortality, marital strife, labor pains, and agriculture. … Consider…“love of nature,” which is used to justify virtually every diet on the market, from gluten-free (modern Frankenwheat is unnatural!) to raw food (cooking is unnatural!). It turns out that the “appeal to nature” is a well-established fallacy, plagued by question begging…in addition to the inherent vagueness of the term natural. Nevertheless, people demand all-natural foods and dutifully avoid unnatural chemicals, oblivious to the irrational foundation of their preferences.
Source: Alan Levinovitz, "The Logical Failures of Food Fads", Slate, 4/21/2015

Try it, you might like it. The author is, of course, promoting a new book, and Harriet "The Skepdoc" Hall has a favorable review of it. Here's a tasty bite:

To many people science is suspect because of the steady stream of scientific reversals on butter, wine, or whatever food appears in the headlines. But [Levinovitz] points out that these are not reversals at all, because nothing was ever established in the first place. The headlines report single preliminary studies that are questionable, not scientific consensus based on an accumulated body of reliable data. True science is humble, cautious, and embraces complexity and uncertainty.
Source: Harriet Hall, "Food Faiths & Diet Religions", Eskeptic, 5/20/2015

Fallacies:

Update: Entirely by coincidence, as far as I know, Brian Dunning of Skeptoid has a podcast today on fads. Not all of the fads that he discusses concern food, but he does deal with juice fads, the dangerous practice of drinking unpasteurised milk, and the anti-gluten hysteria that provides Levinovitz' book its title. Here's a nibble to whet your appetite:

It's hard to say this often enough. Aches and pains usually eventually go away; that's the natural effect of our bodies healing themselves. When they do, our brains tend to credit whatever it was we were doing at the time. …. This is why scientists know that anecdotal experiences, even their own, are terrible ways to learn anything. Our personal experiences are subject to every sort of cognitive error. We have preconceived expectations. We make mistakes and misinterpret things. We have biases.
Source: Brian Dunning, "Listener Feedback: Fads", Skeptoid, 5/26/2015

Check it out.

Fallacies:

May 23rd, 2015 (Permalink)

In the Mail: The Philosophy of Argument and Audience Reception

The latest book by philosopher Christopher Tindale arrived today: The Philosophy of Argument and Audience Reception. Tindale has published a few previous books on argumentation, including one on fallacies and one on sophistry, each apparently from a point of view emphasizing rhetoric. These are all scholarly works and probably too advanced for the beginner, so if you're just starting out Tindale's textbook with Leo Groarke, Good Reasoning Matters, may be the place to start.

Source: Christopher W. Tindale, The Philosophy of Argument and Audience Reception, Cambridge University Press, 2015

May 20th, 2015 (Permalink)

So, what else is new?

Over the years, a number of readers have asked why there is no entry for the so-called "No-true-Scotsman Move" in The Fallacy Files. I've now at least partially remedied that oversight by adding it to the entry for Redefinition as a subfallacy of that fallacy. However, one important thing is missing from the entry, namely, a good real-life example. If anyone has such an example, please let me know.

Fallacy: The No-true-Scotsman Move

Fallacy Files Cafe
May 11th, 2015 (Permalink)

A Puzzle on the Menu

Check out today's menu at The Fallacy Files Cafe. The menu makes two emphatic statements: "Good food is not cheap!" and "Cheap food is not good!" Apparently, if you need to know the price of a dish before you order it, then you can't afford it.

Before proceeding, let's make a couple of things clear: the first statement doesn't mean that just some good food isn't cheap, but that all good food isn't. Moreover, when it says that good food isn't cheap it means that it's expensive. Similarly, the second means that all cheap food isn't good, that is, it's bad.

The puzzle is whether these statements mean the same thing, or something different. Don't just guess! How would you show that your answer is correct? When you think you know, click "Solution" below.

Solution

May 7th, 2015 (Permalink)

What's new?

I've revised and extended the entry for the Quantifier-Shift Fallacy, replacing a cooked-up example with a real-life one. The new example is harder to understand than the previous one, but I think the fact that it comes from an actual argument made by a famous philosopher makes up for the additional difficulty. I've also added a technical appendix for those who know quantificational logic, or are interested in learning more about it.

Fallacy: Quantifier-Shift

May 2nd, 2015 (Permalink)

In the Email Bag

Lawrence Mayes writes:

Dr Henry Marsh, described as a brain or neurosurgeon, has made some frankly daft comments about cycle safety which have got into the press―probably only because they are daft.

Here's a quote from the good doctor that struck Lawrence as "daft"―see the Sources, below: "I see lots of people in bike accidents and these flimsy little helmets don’t help." Back to Lawrence:

There are two aspects to this story that should start alarm bells tinkling straight away. Firstly, we have someone giving an opinion outside his area of expertise and secondly it's all part of a book promotion.

He claimed that he has treated a number of patients involved in bike accidents whose helmets were "too flimsy" to provide any real protection. (I could also truthfully make that claim.) But what Dr Marsh misses is that regardless of the size of this sample it does not include those cyclists involved in accidents whose helmets protected them sufficiently so that they didn't require the intervention of a neurosurgeon nor would he have seen those cyclists who were not wearing helmets and were consequently dead.

This is an example of what's been called "the clinician's error"―see the Resource, below.

There is also the puzzling statistic coming from Bath University which appears twice in the Independent article; this is the reduction in berth that car drivers give cyclists wearing helmets, firstly as "around three inches" then a few paragraphs on as 8.5cm. The second time around it has had a bit of probabilistic decoration added: "In 2006 Dr Ian Walker…found that drivers were twice as like [sic] to get close to cyclists, an average of 8.5cm, when they were wearing a helmet" which, frankly I find incomprehensible (even if he meant "likely").

Whether the average distances are 2ft 9in and 3ft (or whatever the figures may be) seems, to me, to be largely irrelevant; the important figure is the relative accident figures for helmet wearers versus non-wearers.

Walker's study suggests that wearing a helmet may increase the risk of being hit by some unknown amount, but it can't justify changing one's behavior, since we don't know what the trade-off is between a greater risk of an accident and the protection of the head. Perhaps helmeted cyclists are somewhat more likely to be in an accident than unhelmeted ones, but less likely to be killed or seriously injured.

I draw two conclusions from this: firstly, brain surgeons are not as smart as popularly supposed and secondly you should wear a helmet, otherwise you could end up being treated by Dr Marsh.

In fairness, he's not a rocket scientist.

Sources:

Resource: The Clinician's Error, 3/3/2005

Solution to a Puzzle on the Menu: The two statements on the menu are logically equivalent, that is, logically they make the same claim. If you thought otherwise, it's probably because you were misled by non-logical considerations. "Good food is not cheap" may make you think of expensive gourmet food, whereas "cheap food is not good" may bring to mind fast food hamburgers. However, logically speaking, these are simply the opposite sides of the same coin.

There are many ways to show that these two statements logically say the same thing. First, both statements have the form "all P is non-Q", which is logically equivalent to "no P is Q". However, "no P is Q" is logically equivalent to "no Q is P", by the form of immediate inference known as "conversion". Therefore, "all P is non-Q" is logically equivalent to "all Q is non-P", which is the form of immediate inference called "contraposition". 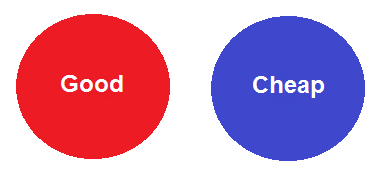Euler Diagram of 'No P is Q'

Another way to show the equivalence is by means of diagrams, of which there are many types. One familiar type of diagram for showing the logical relationship between two classes is the Euler diagram, though it is sometimes inexactly called a "Venn" diagram. An Euler diagram for "no P is Q" shows two non-overlapping circles, as shown. If we let the red circle stand for the class of good food and the blue circle represent the class of cheap food, then the diagram shows that all good food is non-cheap, that is, no good food is cheap. However, it just as much shows that no cheap food is good to eat, that is, that all cheap food is non-good. 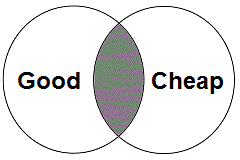No P are Q.

A Venn diagram can also be used to show the logical relationship between two classes. In this case, the shading shows that the overlapping region between the two classes is empty, which means that nothing is in both the good food and cheap food classes. As is the case for the Euler diagram, this single diagram can represent both statements, showing that they make the same logical claim.

Finally, for those who know quantificational logic, "all good food is non-cheap" can be represented as:
∀x[Good(x) → ¬Cheap(x)], where the quantifier ranges over food. This is logically equivalent to:
∀x[¬¬Cheap(x) → ¬Good(x)], by contraposition. Eliminating the double negation gives:
∀x[Cheap(x) → ¬Good(x)], which represents "all cheap food is non-good".

Sources:

Resources:

Check it Out: Unless you're very knowledgeable about crime statistics, you probably have no idea whether these statistics are plausible for the turn of the millennium. So, unlike previous plausibility checks we've done, it's unlikely that you could use benchmark statistics to check these numbers. However, there is an additional way of checking statistics that we used in the previous sanity check―see the Resource, below―namely, cross-checking.

Cross-checking can only be done when we have more than one number to check, but here we have two. To cross-check two numbers we check one against the other for consistency. However, these two cannot be directly compared because one is given in terms of seconds while the other is in terms of a year. Thus, we need to convert one of the numbers into units that match the other so as to directly compare them. Of course, there are two ways to do this:

  1. If you're like me, you have no idea how many seconds there are in a year, except that it must be a lot. However, you do know that there are 60 seconds in a minute, 60 minutes in an hour, 24 hours in a day, and 365 days in a year, excluding leap year. From these facts, we can use multiplication to determine that there are 31,536,000 seconds in a non-leap year. Now, if we divide by 12 we will get the number of victims in a year, given one every twelve seconds, namely, 2,628,000. Clearly, this is much greater than 900,000; in fact, it's nearly 3 times the figure cited by President Clinton.
  2. The other way to figure this is to divide the total number of seconds in a year by the alleged yearly total of 900,000 victims to get the number of seconds per victim, which is slightly over 35 instead of 12. Again, the figure is nearly thrice what Clinton gave.

So, these two numbers are inconsistent, which means that at least one of them must be wrong. According to David Murray, Joel Schwartz, and S. Robert Lichter, in whose book I found this example―see Source 2, above―both numbers are incorrect (p. xiii). In fact, they claim that Clinton first used these numbers in 1995, after which they were publicly criticized and subsequently retracted (p. xiv). Nonetheless, they reappeared five years later in this radio speech.

This example underlines some important points about public statistics:

Resource: Sobriety Check, Part 2, 3/3/2015

Previous Month | RSS/XML | Current | Next Month