Previous Month | RSS/XML | Current | RSS/XML | Next Month
WEBLOG
September 30th, 2021 (Permalink)
The Lab Leak Debate & Ideas Vs. Ideology
- Ashley Rindsberg, "Did the New York Times stifle lab leak debate?", Unherd, 8/2/2021.
In the opening months of the pandemic, the lab leak hypothesis was actively discredited by the media and scientific establishment, with anyone associated with it smeared as "racist". The question we have to ask now is how, and why, did this happen?
To a great extent, I believe the answer lies with the world's most powerful news outlet, the New York Times. At the start of the pandemic, the Times set the news and policy agenda on the lab leak hypothesis, discrediting it and anyone who explored it. The Times did so while taking money from Chinese state-owned propaganda outlets…and while pursuing long-term investments in China that may have made the paper susceptible to the CCP [Chinese Communist Party]'s strong-arm propaganda tactics in the first months of the pandemic. … Of course, over the past year newspapers across the world have fallen for the CCP's distorted Covid-19 narrative. And there is no evidence to suggest that the CCP did put pressure on the Times.
Rindsberg's case against the Times here and in the remainder of the article is circumstantial: he shows that there were serious conflicts of interest involving the Times' business dealings with China, but there's no direct evidence that China brought pressure on the paper, as he here admits, or that the paper tailored its coverage to please the Chinese. However, the conflicts of interest are themselves causes of concern. Here's an example of the other, even weaker, part of his case:
Starting in early 2020, when little was known about the virus―and nothing about its origins―the Times adopted a stridently anti-lab leak stance. In its first report on the topic…the Times stigmatised lab leak as a "fringe theory". Once the story was published, its reporter took to Twitter to describe it as "the kind of conspiracy once reserved for the tinfoil hatters".
Only one week prior, another outlet made strikingly similar claims. In an editorial, the CCP-owned China Daily thundered…[against] "malicious rumors"…. The Times, echoing China Daily, also cast the lab leak hypothesis as a "rumor". Over the months, the Times's coverage grew even more strident―and more in line with Chinese propaganda. …
In fact, the Times appears to have been so enthusiastic in its attempts to discredit the lab leak hypothesis that Chinese propaganda outlets promoted its reporting on social media. In April 2020, for instance, the Times published an article…. Within minutes, a China Daily columnist retweeted the story and parroted its central claim.
This is the sort of McCarthyist guilt by association argument that was used against liberals who supported the civil rights movement in the '50s and '60s. Just because the Times and China Daily took the same position doesn't mean either that the position is wrong or that they're in cahoots. The position may well be wrong, and it was certainly a mistake to dismiss the possibility of a lab leak as a hypothesis, but it isn't necessary to drag in parallels between the Times' coverage and Chinese propaganda to point this out.
Back to the Times' conflicts of interest:
In investing so heavily in China, the Times unintentionally handed the rapacious CCP an editorial lever to sway coverage. The Times learned this first-hand when, in 2012, the CCP blocked Chinese access to the Times online in retaliation for an unfavourable article on the family finances of China's outgoing premier…. The Times set out on a year-long "lobbying" effort to restore coverage that included meetings with Xinhua, the parent of China Daily.
Today, however, just as the tide is turning on the lab leak debate, so too is the Times's approach to the subject. Last summer, the Times abruptly ended its advertising relationship with Chinese state media outlets…. And in recent months, it has published a handful of articles quoting scientists who believe we should take seriously the prospect of a lab leak. But does this excuse the paper's behaviour at the start of the pandemic?
No, of course not, but it's good news. We've already seen how some large media companies are willing to kowtow to Chinese censorship demands in order to do business in China. Hopefully, the Times has now disengaged itself from such ties so that the same thing won't happen to it.
As regular readers of this weblog will know, I'm no fan of The New York Times, but I'm also no fan of McCarthy-style smears.
The second front in the advance of censorship is academia. Here's its latest victory:
- Peter Boghossian, "My University Sacrificed Ideas for Ideology. So Today I Quit.", Common Sense with Bari Weiss, 9/8/2021
Over the last decade, it has been my privilege to teach at [Portland State University]. … But in addition to exploring classic philosophers and traditional texts, I've invited a wide range of guest lecturers to address my classes…. I invited those speakers not because I agreed with their worldviews, but primarily because I didn't. From those messy and difficult conversations, I've seen the best of what our students can achieve: questioning beliefs while respecting believers; staying even-tempered in challenging circumstances; and even changing their minds.
I never once believed―nor do I now―that the purpose of instruction was to lead my students to a particular conclusion. Rather, I sought to create the conditions for rigorous thought; to help them gain the tools to hunt and furrow for their own conclusions. This is why I became a teacher and why I love teaching.
But brick by brick, the university has made this kind of intellectual exploration impossible. It has transformed a bastion of free inquiry into a Social Justice factory whose only inputs were race, gender, and victimhood and whose only outputs were grievance and division.
Students at Portland State are not being taught to think. Rather, they are being trained to mimic the moral certainty of ideologues. Faculty and administrators have abdicated the university’s truth-seeking mission and instead drive intolerance of divergent beliefs and opinions. This has created a culture of offense where students are now afraid to speak openly and honestly.
I noticed signs of the illiberalism that has now fully swallowed the academy quite early during my time at Portland State. I witnessed students refusing to engage with different points of view. Questions from faculty at diversity trainings that challenged approved narratives were instantly dismissed. Those who asked for evidence to justify new institutional policies were accused of microaggressions. And professors were accused of bigotry for assigning canonical texts written by philosophers who happened to have been European and male. …
I decided to study the new values that were engulfing Portland State and so many other educational institutions―values that sound wonderful, like diversity, equity, and inclusion, but might actually be just the opposite. The more I read the primary source material produced by critical theorists, the more I suspected that their conclusions reflected the postulates of an ideology, not insights based on evidence. … And it became increasingly clear to me that the incidents of illiberalism I had witnessed over the years were not just isolated events, but part of an institution-wide problem. The more I spoke out about these issues, the more retaliation I faced. …
I eventually became convinced that corrupted bodies of scholarship were responsible for justifying radical departures from the traditional role of liberal arts schools and basic civility on campus. There was an urgent need to demonstrate that morally fashionable papers―no matter how absurd―could be published. …
I believed then that if I exposed the theoretical flaws of this body of literature, I could help the university community avoid building edifices on such shaky ground. … I continued to believe, perhaps naively, that if I exposed the flawed thinking on which Portland State's new values were based, I could shake the university from its madness. …
This was shown over twenty-five years ago by the Sokal hoax3. Another thing that was shown indirectly by that hoax is something that ought to be obvious: you can't reason with people who don't believe in reason. Apparently, you can't even embarrass them.
This isn't about me. This is about the kind of institutions we want and the values we choose. Every idea that has advanced human freedom has always, and without fail, been initially condemned. As individuals, we often seem incapable of remembering this lesson, but that is exactly what our institutions are for: to remind us that the freedom to question is our fundamental right.
I don't blame Boghossian for quitting, but it is nonetheless a shame. He was at least trying to do exactly what an educator is supposed to do, namely, teach his students how to think, not what to think. Forcing him out is a defeat for what used to be known as "liberal education".
"Liberal education" does not mean indoctrination in a "liberal" political ideology, but the education that is appropriate for a free person. "Liberal", in this use, means "of, pertaining to, or befitting a free person" and descends from the Latin word "liber", meaning "free", from which we also get our word "liberty"4. Liberal education is education for liberty. Without it, it will be harder to retain what liberty we have left against the forces of illiberal indoctrination.
Censorship is again the theme of this month's recommended readings. I wish it didn't have to be. There are two fronts in the advance of censorship in our society: the media and academia. First, the media:
In June's "Recommended Reading"1, we saw how Chinese propaganda and censorship has infiltrated America's news media, and the following article discusses how it may have affected the most august American news organization of them all. It's by the author of The Gray Lady Winked, which I reviewed here last month2.
Notes:
- The Tank Man & Speaking Out Against Lockdowns, 6/30/2021
- Book Review: The Gray Lady Winked, 8/23/2021
- See: The editors of Lingua Franca, The Sokal Hoax: The Sham That Shook the Academy (2000)
- "What Exactly Is a 'Liberal'?", Merriam-Webster, accessed: 9/30/2021
Disclaimer: I don't necessarily agree with everything in these articles, but I think they're worth reading as a whole. In abridging them, I have sometimes changed the paragraphing and rearranged the order of the excerpts in order to emphasize points.
September 29th, 2021 (Permalink)
A trillion here, a trillion there, and pretty soon you're talking about real money.1
No number is big or small in itself. I'm not referring to the fact that "big" and "small" are vague concepts, though they are. Rather, I mean that whether a number is big, small, or in-between depends on what you're talking about. Seven may seem like a small number, but not if you're talking about human height in feet. Of course, some numbers are bigger than others: a million is definitely a larger number than seven. So, whenever you wonder whether a number is big or small, you should ask: relative to what? A million may seem like a large number, but not if you're dealing with dollars of federal spending. These days, even a billion dollars is peanuts to the federal government.
One of the uses of numbers is to compare the sizes of sets of things, but we can't do this well if we don't have a sense of the relative sizes of the numbers. Most of us don't have a good sense of the size of any number ending in "-illion", because we have little personal experience with numbers of such size. We suffer from "number numbness"2 when confronted by numbers in the millions, billions, and trillions, which is the paralyzing effect that very large or extremely small numbers have on our brains.
In particular, few of us have experience with amounts of money greater than a few thousand dollars, and thus no sense of the size of a million dollars, let alone a billion or a trillion. A trillion might as well be a gazillion for all it means to us. However, to put it in a bit of perspective, a trillion is a thousand billion, which is a thousand million; so a trillion is a million million. Also, it may help to at least write out $3.5 trillion dollars with all the zeros, rather than just use the number "trillion", so here it is: $3,500,000,000,000.
I mention the number 3.5 trillion, because that's the price tag in dollars of the federal "reconciliation" bill that has been so much in the news3. "Reconciliation" refers to the recondite legislative process whereby the House of Representatives and the Senate somehow manage to merge their separate bills into a single one4. No one knows exactly what is in the resulting bill, except that it is a grab-bag of taxing and spending. I mean that, literally, no one knows; the current bill is almost 2,500 pages long5, which is a big number for the length of a legislative bill. To put that number into perspective, if you could read the bill at the rate of a page per minute, which is fast, it would still take over forty hours to read. So, there's no way that any one person has read the whole thing carefully.
Even the president of the United States doesn't appreciate the size of a trillion dollars, for he recently made the following statement: "Trillionaires and billionaires are doing very, very well…6." But there are no trillionaires7. The current richest person on Earth is Jeff Bezos, who has a fortune of less than $200 billion, which may sound like a lot, but that's only a fifth of a trillion. So, he's still got a long way to go to become a trillionaire.
Part of numeracy is developing a "number sense" in place of number numbness, that is, developing a feel for the relative sizes of numbers. One way to do so is to learn how to "divide and conquer", that is, to divide a large number by some other number in order to produce a number small enough to "conquer". Of course, the divisor must make sense when dividing the large number. For instance, it's often helpful to divide a large number by the population of the world, a particular country, or some other geographical unit; the result is a ratio "per capita"―that is, "by the head" in Latin8. So, let's do this with the price tag on the reconciliation bill.
A "landmark" number is a statistic that is useful enough to remember. A geographical landmark helps us to find our way around the landscape, whereas a landmark number can help us navigate the statistical landscape. One such number is the current population of the United States, which is easy to remember: about a third of a billion people9. So, to figure the amount per capita of the reconciliation bill, divide 3.5 trillion by 330 million. You'll probably want to use a calculator.
If $3.5 trillion were distributed equally to every man, woman, and child in the United States, it would come to about $10,500 a head, or over $42,400 for a family of four. While $42K is sofa change to the federal government, it is a large sum for most American families. Wouldn't they rather have the government send them a check for their share, rather than spend it on whatever pork barrel projects are funded in the bill?
Any way you look at it, $3,500,000,000,000 is a lot of money. Could Congress get away with trying to spend so much if the American people really understood just how much it is?
Notes:
- The title is based on the statement: "A billion here, a billion there, and pretty soon you're talking about real money", which is usually falsely attributed to Senator Everett Dirksen, according to Ralph Keyes, and is here adjusted for inflation. See: The Quote Verifier: Who Said What, Where, and When (2006), pp. xix & 13-14. This entry is based, in part, on the following entries:
- In the Headlines, 7/16/2009.
- A New Book for a New Year: Is That a Big Number?, 1/5/2019.
- Beyond Innumeracy, 3/7/2020.
- Douglas R. Hofstadter, "On Number Numbness", Metamagical Themas (1985), pp. 115-135.
- See, for instance: Kristin Wilson, "House Budget Committee votes to pass the $3.5 trillion spending bill", CNN, 9/25/2021.
- Eric McDaniel & Kelsey Snell, "A $3.5 Trillion Question: What Is Budget Reconciliation? Here's An Explainer", National Public Radio, 9/14/2021.
- Andrew Solender, "Pelosi Says It's 'Self-Evident' Reconciliation Spending Will Be Less Than $3.5 Trillion", Forbes, 9/26/2021.
- "Remarks by President Biden on the COVID-19 Response and the Vaccination Program", The White House, 9/24/2021.
- Dan Evon, "Do Trillionaires Exist?", Snopes, 9/24/2021.
- Eugene Ehrlich, Amo, Amas, Amat and More: How to Use Latin to Your Own Advantage and to the Astonishment of Others (1985).
- "What is the current population of the United States of America?", Wolfram Alpha, accessed: 9/29/2021.
September 19th, 2021(Permalink)
What's New? The Fallacy of the Sheep is!
While writing the previous entry I was somewhat surprised to discover that it was the fourth example over the last ten years of the fallacy of the sheep, yet I didn't have a separate entry for that fallacy. So, now I've filled that lacuna. You can access the new entry from either the Taxonomy on the Main Menu, or the drop-down menu of the alphabetized fallacy entries, both available in the navigational frame to your left. Check it out!
September 16th, 2021 (Updated)(Permalink)
"Breakthrough" Infections and the Fallacy of the Sheep
…[T]he operator of a diner…offered rabbit sandwiches at a remarkably low price. When questioned about it, he admitted that he used some horse meat to keep his costs down. "But I mix 'em fifty-fifty," he avowed. "One horse to one rabbit."1
In the last few months we've started hearing a lot about "breakthrough" infections. Google Trends shows that the number of searches for the phrase "breakthrough infection" was almost none before April of this year, then peaked in the first week of last month, has declined some since, but remains much higher than before April2. What exactly is a "breakthrough" infection?
A breakthrough infection is simply one in which a vaccinated person becomes infected with the virus the vaccine protects against; it does not mean that the person has any symptoms of the disease3. Since no vaccine is 100% effective in preventing infection, there will always be some breakthrough infections.
Nonetheless, recent events have led to some alarm about coronavirus breakthrough infections: in late June, it was reported that nearly half of new cases in Israel were in people who were vaccinated4, and 75% of those infected in Provincetown, Massachusetts a month later were also vaccinated5.
Some people have misinterpreted these statistics to mean that the vaccinated are just as likely, or even more likely, to become infected than the unvaccinated6. Doing so, however, commits the fallacy of the sheep7.
You may have heard the old riddle: Why do white sheep eat more than black sheep? Because there are more of them. It's not a very good riddle, but it illustrates an important point. When comparing two or more classes of things, you should take into consideration the size of the classes compared. Unless the two classes are the same size, comparing the absolute numbers of a characteristic, such as an infection, between the two classes will be misleading8.
In the case of Israel noted above, the fact that half of those infected were vaccinated and half were unvaccinated, does not mean that the former were just as likely to be infected as the latter. Israel has a high rate of vaccination, with about two-thirds of Israelis having received at least one dose of a vaccine, and about 90% of those being fully vaccinated, at the time of the report9. This means that there were at least twice as many vaccinated Israelis than unvaccinated, yet only half of the new cases were in those vaccinated. Similarly, close to 95% of the population of Provincetown was vaccinated, yet only three-quarters of those infected10. So, there were more white sheep than black ones.
It's likely that we will see more breakthrough infections in coming months as the rate of vaccination continues to increase. So, when you read reports about breakthrough infections in a particular area, always look for the rate of vaccination there. The higher that rate, the higher the percentage of all infections will be breakthrough ones.
Update (9/22/2021): The United States just passed another "grim milestone"; here's how Newsweek reports it:
Deaths related to COVID-19 in the U.S. have reached 676,000, surpassing the number that died during the Spanish Flu pandemic of 1918. Until now, the Centres for Disease Control and Prevention (CDC) had considered the influenza epidemic of 1918 to be the worst pandemic in modern history. … In the U.S. alone the 1918 influenza epidemic killed an estimated 675,000, around one in five people who contracted the virus. … The global spread of the 1918 flu is often referred to as "the forgotten pandemic" because it was overshadowed by the First World War…. Just as it was once overshadowed by WWI, the 1918 pandemic has now been eclipsed by COVID-19. According to The New York Times COVID map, the number of deaths in the U.S. during this current pandemic has topped the number reached by the Spanish Flu.11
As far as I can tell, the CDC still considers the Spanish Flu "the worst pandemic in modern history", specifically calling it "the most severe pandemic in recent history"12. The page from which I take that quote is from a few years ago, but it hasn't been updated due to the latest "grim milestone". Moreover, I doubt that it will be updated, at least not to claim that COVID-19 is worse than the Spanish Flu, and here's why.
I mentioned in the "Exposure" section of the new entry for the Fallacy of the Sheep, q.v., that you need to be wary of comparing statistics from the past and present that may be affected by the increase of population over time. This is what makes the above Newsweek report a perfect example of the fallacy, since it compares the absolute numbers of deaths from COVID-19 with those of the Spanish Flu from over a hundred years ago, without any mention of the difference in population.
The population of the United States in 1918 was 103 million13, whereas it is currently 331 million14. Thus, the 1918 population was less than a third of what it is today, which means that the death toll of COVID-19 would have to be three times as much as the current "grim milestone" to match the death rate of the Spanish Flu.
So, COVID-19 is not now the worst pandemic in modern history, as suggested by Newsweek. It's not even close.
Notes:
- Darrell Huff, The Complete How to Figure it: Using Math in Everyday Life (1996), p. 391.
- "breakthrough infection", Google Trends, accessed: 9/16/2021.
- See:
- Sanjay Mishra, "What is a breakthrough infection? 6 questions answered about catching COVID-19 after vaccination", The Conversation, 7/28/2021
- Emily Willingham, "'Breakthrough' Infections Do Not Mean COVID Vaccines Are Failing", Scientific American, 8/4/2021
- Marianne Guenot, "Israel says the Delta variant is infecting vaccinated people, representing as many as 50% of new cases. But they're less severe.", Business Insider, 6/24/2021.
- Kristina Fiore, "No, Most COVID Infections Are Not Occurring in Vaccinated People", MedPage Today, 8/6/2021.
- Jessica McDonald, "Posts Misinterpret CDC's Provincetown COVID-19 Outbreak Report", Fact Check, 8/6/2021.
- Stephen K. Campbell, Flaws and Fallacies in Statistical Thinking (1974), pp. 101-104. For other examples of the fallacy, see:
- The Riddle of the Sheep, 10/13/2011
- Ron Paul on Drugs, 11/26/2011
- Risky Thinking, 5/27/2018
- Katelyn Jetelina calls the mistake "base rate bias" or "the base rate fallacy"―see the entry for the latter from the drop-down menu to your left. I'm not sure what "base rate bias" refers to, but I don't think that this is an example of the fallacy of the same name. The base rate fallacy and the fallacy of the sheep are similar, but the latter is a better match for the mistake committed here. See: Katelyn Jetelina, "Israel, 50% of infected are vaccinated, and base rate bias", Your Local Epidemiologist, 6/27/2021.
- Edouard Mathieu & Hannah Ritchie, "Vaccinations and COVID-19―Data for Israel", Our World in Data, 2/8/2021. See the charts; accessed: 9/16/2021.
- Ellen Barry & Beth Treffeisen, "'It's Nowhere Near Over': A Beach Town's Gust of Freedom, Then a U-turn", The New York Times, 7/31/2021. The outbreak took place due to an influx of visitors to the town, and 80% of the infections due to the event were in such visitors, but I haven't been able to find out what percentage of those visitors were vaccinated. Presumably that percentage was less than 95%, so that the overall percentage of vaccination among those in the town at the time of the outbreak would also be less, but how much less I don't know.
- Robert Lea, "How Many Americans Died From Spanish Flu and How Did the Pandemic End?", Newsweek, 9/21/2021. Paragraphing suppressed.
- "History of 1918 Flu Pandemic", Centers for Disease Control and Prevention, 3/21/2018.
- "What was the population of the United States in 1918?", Wolfram Alpha, accessed: 9/22/2021.
- "What is the current population of the United States?", Wolfram Alpha, accessed: 9/22/2021. This is a useful landmark number―that is, a number that can help you navigate the statistical landscape―and it's easy to remember since it's about one-third of a billion.

September 11th, 2021 (Permalink)
Play with Your Mind, Part 2
Note: Here's an example of the second of the two types of logic puzzle found in this month's new book, Games for Your Mind1, namely, a "knights and knaves" puzzle. Specifically, it's from the master of this type of puzzle, Raymond Smullyan:
…Alice [and] the Duchess…had the following remarkable conversation."The Cheshire Cat says that everyone here is mad," said Alice. "Is that really true?"
"Of course not," replied the Duchess. "If that were really true, then the Cat would also be mad, hence you could not rely on what it said."
This sounded perfectly logical to Alice.
"But I'll tell you a great secret, my dear," continued the Duchess. "Half the creatures around here are mad―totally mad!"
"That doesn't surprise me," said Alice, "many have seemed quite mad to me!"
"When I said totally mad," continued the Duchess, quite ignoring Alice's remark, "I meant exactly what I said: They are completely deluded! All their beliefs are wrong―not just some, but all. Everything true they believe to be false and everything false they believe to be true." …
"What about the sane people around here?… I guess most of their beliefs are right but some of them are wrong?"
"Oh, no, no!" said the Duchess most emphatically. "That may be true where you come from, but around here the sane people are one hundred percent accurate in their beliefs! Everything true they know to be true and everything false they know to be false."
Alice thought this over. "Which ones around here are sane and which ones are mad?" asked Alice. … "I've always wondered about the March Hare, the Hatter, and the Dormouse," said Alice. "The Hatter is called the Mad Hatter, but is he really mad? And what about the March Hare and the Dormouse?"
"Well," replied the Duchess, "the Hatter once expressed the belief that the March Hare does not believe that all three of them are sane. Also, the Dormouse believes that the March Hare is sane."2
Are the Mad Hatter, March Hare, and the Dormouse mad or sane?
All three are mad. Here's Smullyan's explanation:
Suppose the Hatter is sane. Then his belief is correct, which means that the March Hare does not believe that all three are sane. Then the March Hare must be sane, because if he were mad, he would believe the false proposition that all three are sane. Then the Dormouse, believing that the March Hare is sane, must be sane, which makes all three sane. But then how could the sane March Hare fail to believe the true proposition that all three are sane? Therefore it is contradictory to assume the Hatter sane; the Hatter must really be mad.Since the Hatter is mad, his belief is wrong, and therefore the March Hare does believe that all three are sane. Of course the March Hare is wrong (since the Hatter is not sane), and so the March Hare is also mad. Then the Dormouse, believing the March Hare is sane, is also mad, and so all three are mad (which is not too surprising!).3
It also wouldn't be too surprising if that explanation drove you mad.
Notes:
- Playing with Your Mind, 9/7/2021
- Raymond Smullyan, Alice in Puzzle-Land: A Carollian Tale for Children Under Eighty (1982), pp. 20-22 & 24-25
- Ibid., pp. 146-147

September 8th, 2021 (Permalink)
Play with Your Mind, Part 1
Here's an example of one of the two types of logic puzzle found in this month's new book, Games for Your Mind1. This one was created by Lewis Carroll of Alice in Wonderland fame2. Consider the following clues:
- Every one who is sane can do Logic.
- No lunatics are fit to serve on a jury.
- None of your sons can do Logic.
Based on the above clues, are any of your sons fit to serve on a jury?
No.
Explanation: This puzzle is one of the type based on the logic of categories, that is, classes of things. So, the first step in tackling such a puzzle is to identify the categories. Usually, each clue will relate two categories, and that's the case for this puzzle. For instance, the first clue relates the category of sane people to that of people who can do Logic. Then, the second relates the category of lunatics to that of people who are fit to serve on a jury. Finally, the last one relates the category of your sons to that of those who can do Logic.
Here's a subtle but important point: it may look as though there are five categories here, but we can get by with only four because lunatics are just people who are not sane. So, when you're identifying categories, always look out for a category that is just the negation of another category.
Here are the four categories and abbreviations of them that I'll use:
- S: Sane people
- L: Those who can do Logic
- J: Those who are fit to serve on a jury
- Y: Your sons
Having identified the categories, it's time to determine the logical relationships between them established by the clues:
- S is contained in L.
- This one is a bit tricky. It says that no one who is insane is fit to serve on a jury. In other words, non-S and J are disjoint, that is, there's no overlap between them. If you think about it, you should see that this is the same thing as saying that all those fit to serve on a jury are sane, that is, J is contained in S.
- Y and L are disjoint.
All of this is preliminary work that must be done before solving the puzzle. There are many different techniques you could use to do so: Aristotelian categorical syllogisms, Euler or Venn diagrams, set theory, quantificational logic, among others. If you don't know any of these techniques, you may be able to think your way to the answer without them. In any case, I'll leave that to you.
Finally, I'll explain how the answer follows from the clues. The easiest way to do so is by means of the following Euler diagram:
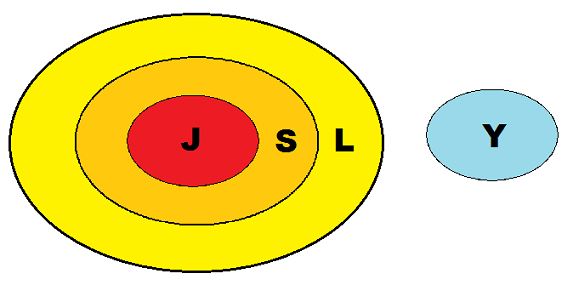
The diagram shows that S is contained in L―clue 1―J is contained in S―clue 2―and Y is disjoint from L―clue 3. So, we can see from the diagram that Y and J are disjoint, which means that none of your sons is fit for jury duty.
Notes:
- Playing with Your Mind, 9/7/2021
- Lewis Carroll, Symbolic Logic and the Game of Logic (1958), pp. 112 & 132

September 7th, 2021 (Permalink)
Playing with Your Mind
Quote: "Among mathematical recreations generally, logic puzzles are the most ecumenical. All that is needed is a bit of patience and some clear thinking. No algebra, geometry, computational skill, or any other sort of specialized knowledge is required. The payoff for solving one, however, is the smile you wear on your face for the rest of the day."1
Title: Games for Your Mind
Subtitle: The History and Future of Logic Puzzles
Author: Jason Rosenhouse
Comment: Rosenhouse is a professor of mathematics who has written a previous book on the Monty Hall problem that I haven't read.
Date: 2020
Summary: Despite its subtitle, this book seems to be more an introduction to logic through puzzles than a discussion of their history or future. It's focused on two types of puzzle, rather than on all those that could be labelled "logic puzzles":
- Puzzles based on Aristotelian categorical logic. In particular, the book concentrates on puzzles created by Lewis Carroll, who is better known as the author of the Alice children's books than as a puzzle creator.
- What are traditionally called "knights and knaves" puzzles in which there are two types of character, "knights" that always tell the truth and "knaves" that always lie. The late Raymond Smullyan was the master of this type of puzzle, writing several books filled with them.
I've offered a number of puzzles of both types here on the weblog, including the recent "New Logicians' Club" puzzles, which are variations on the second type. Other common types of logic puzzle receive only passing mention in the book. You won't find much on Sudoku puzzles, despite the fact that they are currently the most popular type of logic puzzle. However, Rosenhouse has co-written an entire book on them2, so check that out if Sudoku seriously interests you.
Rather to my disappointment, another common type of puzzle that is largely missing is that which often goes by the name "logic puzzle"―there doesn't seem to be a more specific name for them. There are whole books and magazines devoted to this type of puzzle. Familiar examples are the Smith, Jones, and Robinson puzzle, and the Zebra puzzle―Rosenhouse does give a version of the latter as an example.
If you're interested in learning logic, but don't want to take a class or are daunted by the prospect of reading a text book, and if you enjoy puzzles, you might try this approach. You will, in fact, learn much more from working logic problems than just passively reading a book.
What little I've read of the book is clearly and accurately written, though perhaps aimed at a somewhat more sophisticated readership than I would have expected. For instance, there's a section of the first chapter on philosophy of logic3 that I would suggest skipping unless you're really interested in the topic. In fact, it wouldn't hurt to just skip the whole first chapter and get right to the puzzles in chapter 2.
Disclaimer: This book is from late last year, so it's not brand new, but I haven't read it in its entirety yet. My comments above are based on reading a short excerpt and studying its table of contents.
Notes:
- Section 2.2
- Jason Rosenhouse & Laura Taalman, Taking Sudoku Seriously: The Math Behind the World's Most Popular Pencil Puzzle (2012)
- Section 1.2