Previous Month | RSS/XML | Current | Next Month
WEBLOG
February 28th, 2017 (Permalink)
New Book: The Death of Expertise
Thomas M. Nichols has a new book out with the above title, and the subtitle: "The Campaign Against Established Knowledge and Why it Matters". That sounds rather conspiracist: a "campaign"? As I've pointed out previously, sensationalistic titles and subtitles of books may well be provided by the publisher, so I wouldn't necessarily blame them on the author. In fact, he himself begins the Preface by partially retracting the title:
"The death of expertise" is one of those phrases that grandly announces its own self-importance. It's a title that risks alienating a lot of people before they even open the book… I understand that reaction because I feel much the same way about such sweeping pronouncements. Our cultural and literary life is full of premature burials of everything: shame, common sense, manliness, femininity, childhood, good taste, literacy, the Oxford comma, and so on. The last thing we all need is one more encomium for something we know isn't quite dead. While expertise isn't dead, however, it's in trouble. Something is going terribly wrong.
So, hopefully the book is not as alarmist or conspiracy-minded as its title suggests.
Who is Thomas M. Nichols, and what expertise does he have to write this book? According to the brief biography on Amazon, he is a professor of National Security Affairs, an expert on foreign policy, and an undefeated champion on "Jeopardy!". So, he is an expert, but not an expert on expertise itself. But then, who is?
February 21st, 2017 (Permalink)
A Puzzle in Memoriam
Here is a puzzle in memory of the late Raymond Smullyan. It comes from a book whose name I always forget (what is it!?). The puzzle, which comes "From the Files of Inspector Craig" of Scotland Yard, involves figuring out which of a group of suspects are guilty of a crime. Here it is, in Smullyan's words:
This case…involves four defendants, A, B, C, D. The following facts were established:
- If A is guilty, then B was an accomplice.
- If B is guilty then either C was an accomplice or A is innocent.
- If D is innocent then A is guilty and C is innocent.
- If D is guilty, so is A.
Which ones are innocent and which ones are guilty?
February 20th, 2017 (Permalink)
Obituary: Raymond Smullyan
I've just heard that logician and puzzlist Raymond Smullyan died earlier this month at the young age of 97. Smullyan was the master of the knights-and-knaves type of logic puzzle, of which he created many. He was also probably the only logician ever to appear on The Tonight Show with Johnny Carson. He was unique and will be missed.
Resource: Richard Sandomir, "Raymond Smullyan, Puzzle-Creating Logician, Dies at 97", The New York Times, 2/11/2017
Acknowledgment: Thanks to Jim Z. for the notice.
February 17th, 2017 (Permalink)
Quote…Unquote
…Milton Friedman, my hero, was quoted as finding in national service an "uncanny resemblance" to the Hitler Youth Corps. This…occasions only the reply that by that token, all youth programs, including the Boy Scouts, can be likened, in the sense that they have something in common, to the Hitler Youth program, plus the second comment, that because Hitler had an idea, it does not follow that that idea was bad.
Source: William F. Buckley, Jr., Gratitude: Reflections on What We Owe to Our Country (1990), p. 49
February 16th, 2017 (Permalink)
Lesson in Logic 16: The Third Circle
These lessons on Venn diagrams started with a single circle (Lesson 11), then added a second, overlapping one (Lesson 12). As you saw, with a single circle you can only diagram simple statements about a single class, such as "There are no dodos" or "Black swans exist". By adding a second, overlapping circle, you can represent the four traditional categorical statements relating two classes: A, E, I, and O (Lesson 13). Two-circle diagrams can be used to show logical relations between two of these categorical statements, such as equivalence (Lesson 14) and contradiction (Lesson 15). However, arguments in which three classes play a role require the addition of a third circle overlapping the first two. In this lesson, you'll learn how to construct and understand such a diagram.
A single circle divides the universe up into two classes: those things inside the circle and those without; the two, overlapping circles of Venn's primary diagram divide the world into four classes: those things in the first but not the second circle, those in the second but not the first, those in both, and those in neither. You may notice a pattern here.
Q: How many classes will the diagram divide the world into if we add a third circle?
A: Eight. Each time a circle is added doubles the number of subclasses represented in the diagram.
So, look at the diagram; you've probably seen one like it before. It uses colors to represent the three classes and eight subclasses. The three classes represented by the circles are red, blue, and green. Where just two classes overlap the colors of the two circles blend together; for instance, where the red and blue circle overlap outside the green circle, is the color purple. Here is a list of all eight subclasses:
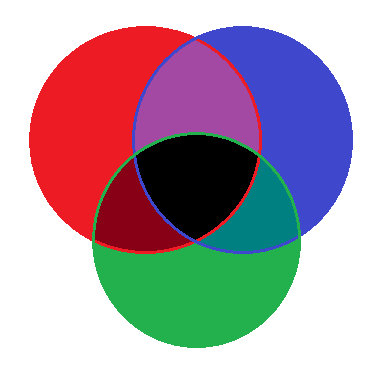
- Red: Those things in the red circle but outside of the blue and green circle.
- Blue: Those things in the blue circle but outside of the red and green circle.
- Green: Those things in the green circle but outside of the red and blue circle.
- Purple: Those things in both the red and blue circles but outside of the green circle.
- Blue-Green: Those things in both the blue and green circles but outside of the red circle.
- Brown: Those things in both the red and green circles but outside of the blue circle.
- Black: Those things inside all three circles.
- White: Those things outside all three circles.
The trick to interpreting a Venn diagram with three circles is to understand where in the diagram each subclass is found. For example, let's suppose that the universe of the diagram represents people, the red circle contains all red-haired people, the blue circle all those with blue eyes, and the green circle members of the Green Party.
Q: Where in the diagram would a member of the Green Party who has brown hair and green eyes be found?
A: In the green subsection at the bottom, outside of the red and blue circles.
Test and increase your understanding of the diagram with the following exercises.
Exercises:
- Where in the diagram would a blond, blue-eyed Democrat be found?
- Travis is a gray-haired, gray-eyed, Libertarian. Where in the diagram is he?
- Leif is a green-eyed redhead but I don't know what his politics are. Where would he be found in the diagram?
- Where in the diagram is Kathleen, a red-headed, blue-eyed woman who just joined the Green Party?
- Where are you in the diagram?
Next Lesson: Learn how to diagram categorical statements on a three-circle Venn diagram.
Previous Lessons:
- Lesson in Logic 11: Class Diagrams, 6/22/2016
- Lesson in Logic 12: Two-Circle Venn Diagrams, 7/16/2016
- Lesson in Logic 13: Categorical Statements, 8/17/2016
- Lesson in Logic 14: Equivalence, 11/15/2016
- Lesson in Logic 15: Contradiction, 12/13/2016
February 13th, 2017 (Permalink)
Headline
How beer brewed 5,000 years ago in China tastes today
Kind of stale, I'm guessing.
February 4th, 2017 (Permalink)
Pretzel Logic Puzzle
Half of the customers at Pete's Gourmet Pretzel Palace prefer their pretzels with mustard. Half of those who use mustard don't also dip their pretzels in melted cheese, while one-fifth of those who don't put mustard on them also don't use cheese. What percentage of Pete's customers dip their pretzels in cheese but not in mustard? If you think you know the answer, click on "Solution", below.
Resource: Using Venn Diagrams to Solve Puzzles, 1/18/2017. This puzzle can be solved using the same techniques discussed in this entry.
February 2nd, 2017 (Permalink)
Book Club: Winning Arguments,
Introduction, Part Deux
In the first book club installment 1, I suggested as an exercise that you analyze the argumentative structure of a passage from the introduction to our book club book. My original intent was to do so at the beginning of this month's installment, then proceed to discuss the first chapter. However, the argument is so interesting and revealing that I think it's worth a separate entry. Also, the first chapter is fairly long, so I want to leave discussion of it to a separate entry. So, for now, we're still in the introduction.
So that you don't have to look back at the previous entry, here's the passage in question again. It contains a single argument, and by analyzing its structure I have in mind determining what its premises and conclusion are. If you haven't done so already, try it now:
Each of us occupies a partial, time-bound perspective and none of us has access to the God's-eye view from which the "big picture" might be seen at a glance. Therefore any statement any of us makes is an argument because, as an assertion that proceeds from an angle, it can always be, and almost always will be, challenged by those whose vision is also angled, but differently so.2
The first thing you should have noticed is the word "therefore" at the beginning of the second sentence. "Therefore" is the paradigm example of an argument-indicator word, that is, it indicates that it is part of an argument. Specifically, "therefore" is a conclusion indicator 3, which indicates that the sentence it begins is the conclusion of the argument and the sentence that it follows is a premise for that conclusion.
Less noticeable, but just as important, is the word "because", which is the other type of argument indicator, namely, a premise indicator 4, which indicates that the sentence that follows it is a premise of the argument. Sandwiched in between "therefore" and "because" is the conclusion of the argument; this is a common type of argumentative structure. Put all this together and you get the following structure:
First Premise: Each of us occupies a partial, time-bound perspective and none of us has access to the God's-eye view from which the "big picture" might be seen at a glance.
Second Premise: As an assertion that proceeds from an angle, any statement any of us makes can always be, and almost always will be, challenged by those whose vision is also angled, but differently so.
Conclusion: Any statement any of us makes is an argument.
Now that the argument's structure is clear, you can proceed to evaluate its cogency. How strong is the logical connection between the premises and the conclusion? Are the premises true?
Unfortunately, there is a confusing use of terminology in the conclusion: What does Fish mean by the word "argument"? This is not only a vital question to answer for evaluating this particular argument, it's an important question for understanding the book as a whole, given that its title is Winning Arguments.
In the usual logical sense of the words "argument" and "statement", the conclusion is false, since the classes of statements and arguments are disjoint, that is, no statements are arguments and no arguments are statements. An argument is a set of statements, rather than a single one.
An alternative meaning of "argument"―call this the "dialectical" sense―is a type of discussion between two or more people, usually based on a disagreement. However, this meaning won't make the argument's conclusion true, since it takes more than a single statement to make a discussion, though a single statement may form the basis for a disagreement that then leads to a dialectical argument.
So, reading the premises of the argument charitably, it seems that what Fish has in mind would be better stated as follows: Any statement any of us makes is arguable―rather than itself an argument. In other words, because none of us sees things from a God's-eye point of view, but from our own particular POV, any statement we make may be challenged, that is, it may form the seed of disagreement that sprouts into an argument, in the dialectical sense.
Is the (logical) argument with this revised conclusion cogent? Notice that this is an argument from analogy. Fish uses a familiar analogy between thought and vision, an analogy that is so common that it may not be immediately apparent that it is an analogy. He talks about "seeing" from different "points-of-view" and "angles", but he's really not concerned with eyesight, rather he's talking about how we think. Our beliefs about the world, and the statements we make about it, come from limited, individual POVs, and thus are always subject to disagreement.
However, if you take this analogy seriously, you'll see that it doesn't really support Fish's conclusion. The fact that we all see things from our own particular vantage point, and that we cannot see the world through another's eyes, does not mean that there isn't much that we all see and agree upon. We often see the same thing from different angles yet agree about what we see. So, Fish's argument is based on a rather weak analogy 5, but we probably shouldn't put too much weight on it at this point since we're still in the Introduction. Perhaps there are stronger arguments to come.
Moreover, I'm not sure why Fish thinks that he needs such a strong conclusion, namely, that every statement is arguable. Isn't it enough that many are? At this point, it seems that all he needs to do is convince us that argumentation is important, and I for one don't really need much convincing on that point. However, perhaps he has bigger fish to fry. 6
Sources & Resources:
- Book Club: Winning Arguments, Introduction, 1/21/2017
- Page 2 in the hardcover edition.
- Lesson in Logic 4: Conclusion Indicators, 4/11/2007
- Lesson in Logic 6: Premise Indicators, 6/12/2007
- Weak Analogy
- Sorry!
Next Installment: Chapter 1. Living in a World of Argument
- In the blue subsection.
- In the white section outside of all three circles.
- We don't have enough information to put him in a specific subsection, but we do know that he is in the red circle―since he has red hair―outside of the blue circle―since he has green eyes. This means that he is either in the red or brown subsections.
- In the black section representing the overlap of all three circles.
- How would I know?
Solution to the Pretzel Logic Puzzle: 40%
Solution to a Puzzle in Memoriam: Here is the answer in Smullyan's words:
The answer is that all of them are guilty. By (3), if D is innocent then A is guilty. By (4), if D is guilty, then A is guilty. So whether D is innocent or guilty, A must be guilty. Hence by (1), B is also guilty. Hency by (2), either C is guilty or A is innocent. But we already know that A is not innocent, therefore C must be guilty. Finally, by (3), if D is innocent then C is innocent. But we have proved that C is not innocent, hence D must be guilty. So all of them are guilty.
Source: Raymond M. Smullyan, What is the Name of this Book? (1978), pp. 71 & 78