Previous Month | RSS/XML | Current | Next Month
WEBLOG
December 31st, 2016 (Permalink)
Book Review: Standard Deviations
Title: Standard Deviations
Sub-Title: Flawed Assumptions, Tortured Data, and Other Ways to Lie with Statistics
Author: Gary Smith
Publisher: Overlook
Date of Publication: 2014
Quote: "Sometimes, the unscrupulous deliberately try to mislead us. Other times, the well-intentioned are blissfully unaware of the mischief they are committing. My intention in writing this book is to help protect us from errors―both external and self-inflicted. You will learn simple guidelines for recognizing bull when you see it―or say it. Not only do others use data to fool us, we often fool ourselves." (P. 5)
Review: Not long ago, I remarked that there seems to have been a spate of books in the last few years about how to detect misinformation on the internet and elsewhere1. This is one of those I mentioned, and it's a good one. With the current concern about the influence of fake news, it's as timely as when it first appeared a couple of years ago.
If you want to learn statistics, I can recommend a few good textbooks, but this is not one of them. That's because it's not a textbook at all, but a book on statistics for us non-statisticians. We may not be statisticians, but we are consumers of statistics. Politicians, activists, advertisers, and others, use statistics to influence us to vote for them, support their causes, or buy their products. Unfortunately, many of these statistics are impostors, and most of us don't know how to separate the statistical sheep from the wolves-in-sheeps'-clothing. If you're not a statistician, then this book's for you.
The author of this book, Gary Smith, is an economist, but he's also authored statistics textbooks. I haven't read any of them, but if they're as good as this non-textbook, I would recommend them as well.
I actually learned some things from this book. I write that with some surprise because I've read several books that cover much the same territory, and some of which were excellent. Not only that, but I've written entries on some of the fallacies discussed by Smith, so that most of what is covered here is familiar ground to me. Here is a selective outline of topics covered in this book:
- "Patternicity"2: This is Michael Shermer's term for "finding meaningful patterns" where there are none3. Smith doesn't use Shermer's term for it, but this is the topic of the chapter. Among other things, you'll learn about a "psychic" octopus that seemingly could pick the winners of soccer games (pp. 7-11).
- Self-Selection Bias & Survivor Bias4: Learn about Abraham Wald and the missing bomber planes, as well as how to search for excellence but not find it. (Chapter 2)
- Charts & Graphs: And how to lie with them5. (Chapter 5)
- The Gambler's Fallacy: Pp. 125-126, Chapter 106.
- "Hot Hands": Do basketball players sometimes get a "hot hand"? Maybe so, but what about craps players? Basketball is a game of skill, whereas craps is a game of chance. There is evidence that players do get "hot" or "cold" in games requiring skill, but the hot or cold hand in games of chance is an illusion. See, pp. 127-1357.
- Regression to the Mean: Chapter 98.
- The Texas Sharpshooter: Chapter 119.
Lest I seem unduly positive in this review, I will mention one mistake that I think Smith makes: In chapter 6, he discusses a well-known problem in probability theory sometimes known as the "boy-girl paradox" (pp. 93-96). If you're unfamiliar with it, I based a puzzle last Christmas on this very paradox10. While I'm not an expert, I gave as the solution to that puzzle what Smith disparagingly refers to as the "expert's" answer. At first, I was impressed by Smith's arguments but, counterintuitive as it may seem, in this case I think that the experts were right. Oh, well, nobody bats 1.000.11
Recommendation: Highly recommended for non-statisticians and other non-experts.
Sources & Resources:
- New Book: A Field Guide to Lies, 10/19/2016
- Check 'Em Out, 1/21/2010
- Michael Shermer, "Patternicity: Finding Meaningful Patterns in Meaningless Noise", Scientific American, 12/1/2008
- New Book: Standard Deviations, 8/30/2014
- Charts & Graphs: The YY Graph, 11/19/2013. See the previous entries listed at the bottom of this entry.
- The Gambler's Fallacy
- The Hot Hand Fallacy
- The Regression Fallacy
- The Texas Sharpshooter Fallacy
- A Puzzle for Christmas, 12/25/2015
- See the correction appended below.
Correction (7/26/2019): At the end of the last paragraph of the review, above, I wrote: "Oh, well, nobody bats 1.000." "Nobody" includes me, too. I've recently revisited the mistake that I thought Smith made in his discussion of the "boy-girl paradox" and now think that Smith was right, after all. See the entry linked under note 10, above, for details.
By the way, Smith claims repeatedly that the experts gave the wrong answer to the version of the puzzle he discusses, whereas common sense was correct about it. Well, as I said in the review, I'm not an expert. However, it would be more accurate to say that some experts were wrong about it but other experts, such as Smith himself, were right. Anyway, the fact that Smith was right about this so-called paradox is all the more reason why this is an excellent book. Perhaps Smith did bat 1.000.
December 25th, 2016 (Permalink)
A Christmas Puzzle Present
The Smith family has four children in all, each a year apart in age. Santa Claus brought each child a different type of puzzle for Christmas, including a book of logic puzzles. Each present was wrapped in a different color ribbon, one of which was gold, and tied with a bow on top. The four children took turns opening their presents on Christmas morning.
Annie was the first to open her present, the thirteen-year-old sibling was second, a book of acrostics was the third present opened, and the present topped with a green ribbon―which was not the jigsaw puzzle―was the last to be opened, though not by Charlie.
Bonnie, who is not the oldest sibling, received a present sporting a shiny silver ribbon.
Donnie, who did not receive the book of crossword puzzles as his gift, is a year younger than the sibling who received the jigsaw puzzle.
The gift with a red ribbon was unwrapped immediately after the twelve-year-old's present was opened.
From the above information, can you determine the order in which each child opened his or her present, the age of each child, the type of puzzle each received as a gift, and the color of ribbon in which the puzzle was wrapped?
| Order | Name | Age | Puzzle | Ribbon |
|---|---|---|---|---|
| 1. | Annie | 12 | jigsaw | gold |
| 2. | Charlie | 13 | crossword | red |
| 3. | Bonnie | 10 | acrostic | silver |
| 4. | Donnie | 11 | logic | green |
December 22nd, 2016 (Permalink)
New Book: Winning Arguments
Stanley Fish―yes, that Stanley Fish―has a new book out titled Winning Arguments: What Works and Doesn't Work in Politics, the Bedroom, the Courtroom, and the Classroom. This is a popular topic for books, since everybody wants to "win" arguments, and the Fallacy Files library contains at least five books with similar titles:
- Madsen Pirie's How to Win Every Argument 1, the updated and expanded edition of the classic Book of the Fallacy2.
- An earlier book with the same title by Nicholas Capaldi, though like Pirie's book it originally had a different title: The Art of Deception3.
- Lawyer Gerry Spence's How to Argue and Win Every Time4.
- How to Win Arguments, by the late publisher of National Review, William Rusher, with the more modest subtitle: "More Often Than Not". So, a more accurate title for the book would have been: How to Win Most Arguments.
- Finally, the most modestly titled book is How to Win an Argument5, by philosopher Michael Gilbert. Apparently, Gilbert is not claiming that his book will teach you how to win every argument, or even most, and if you win just one you'll have no cause for complaint.
Resources:
- New Book, 12/2/2007
- Good News, 9/27/2004
- In the Mail, 10/23/2012
- Check it Out, 2/24/2007
- New Book: Arguing with People, 10/21/2014
December 19th, 2016 (Permalink)
Fake News Headline
Fake news is now all the rage, or at least worrying about it is. You'd think from all the current handwringing that people have just discovered that there is fake news on the internet. However, fake news is older than the internet; in fact, it's as old as news itself. Here's a headline from just a few years ago:
Scientific study reveals conspiracy theorists the most sane of all
This is one of a few similar headlines each found on various different fake news sites, all referring to the same study. Why is this fake news? The study had nothing to do with the sanity or lack thereof of conspiracy theorists (CTists). Don't believe me? Would you believe a co-author of the study?
This study has recently been linked to as a demonstration that people who believe 9/11 conspiracy theories are "more sane" than people who don't. The study has no bearing on mental health, and this claim about "sanity" relies on wishful misinterpretation of the results.6
Don't believe a co-author of the study? Would you believe your own lying eyes? If so, see the study itself 5. As you can easily see for yourself, the words "sane", "insane", "sanity" and "insanity" do not even appear in it.
If the study itself had nothing to do with the comparative sanity of CTists, where did the authors of these articles get the idea that it did? It appears that they all trace back to a single source, namely, an article by Kevin Barrett on the PressTV website1.
What is PressTV? It is a TV network funded and controlled by the government of Iran, that is, it's a propaganda site2. Also, the president of Iran at the time the article was written was a notorious CTist who has called the Holocaust a "myth"4, and Iran has hosted conferences questioning its reality3.
Who is Kevin Barrett? Well, he's a CTist himself, specifically of the 9/11 variety. This fact, of course, was not revealed in the little biographical blurb at the bottom of his fake news article. In addition to writing fake news for PressTV, Barrett has also appeared on the network.
What was the "wishful misinterpretation" that led Barrett to claim that the study showed that CTists are "saner" than others?
…[A]mong people who comment on news articles, those who discount official government accounts of events like the 9/11 attacks and the assassination of John F. Kennedy outnumber believers by more than two-to-one. That means the pro-conspiracy commenters are those who are now expressing what is considered conventional wisdom, while the anti-conspiracy commenters represent a small, beleaguered minority that is often scoffed at and shunned.1
So, apparently Barrett thinks that the fact that CTists outnumbered non-CTists on the specific comment threads to the news articles examined in the study somehow shows that they are now in the majority, and that "sanity" is simply whatever the majority believes. This, of course, is wrong on both counts.
Even if the study had been about sanity, it could not have correctly concluded anything about CTists and non-CTists in general. Here's the co-author's description of the study design: "In this study…we collected over 2000 comments from online news stories about 9/11―the ones that tried to persuade people one way or another regarding whether the attacks were the result of a government conspiracy."6 So, the study was based on a sample of online comments, which is not a representative sample of people in general, but only of those who are inclined to leave online comments to news stories. It is very likely that such people are at least more strongly motivated about the subject of the story than those who choose not to comment, and so they are not representative of CTists in general, let alone people in general.
Putting aside the issue of comparative sanity, this example is consistent with a point I've made before about CTists―or, perhaps it's more a point about those who pander to CTists for gain. While CTists are quick to claim that we are all being lied to by the powers that be, one of the most conspicuous traits of those who write articles promoting such theories is their mendacity or at least lack of concern about the truth.
It's not hard to find out that the study in question has nothing to do with sanity or insanity, yet there are still many versions of uncorrected articles with the same or similar headlines. Admittedly, the sites that host such articles are disreputable ones―and would be disreputable for no other reason than hosting the articles. I won't link to any of them since I don't want to help the Google ranking of fake news sites, but if you want to check them for yourself―which is a practice that I generally recommend―you can do so by searching on the headline given above, or related keywords.
Sources:
- Kevin Barrett, "New studies: 'Conspiracy theorists' sane; government dupes crazy, hostile", PressTV, 7/12/2013. This is the Wayback Machine's archive of the page from PressTV, which appears to be no longer available on PressTV's website, so linking to this page doesn't help its Google ranking.
- Douglas Murray, "Push off now, Press TV, and take your conspiracy theories with you", Spectator, 1/20/2012.
- Robert Tait, "Holocaust deniers gather in Iran for 'scientific' conference", The Guardian, 12/11/2006.
- Karl Vick, "Iran's President Calls Holocaust 'Myth' in Latest Assault on Jews", The Washington Post, 12/15/2005.
- Michael J. Wood & Karen M. Douglas, "'What about building 7?' A social psychological study of online discussion of 9/11 conspiracy theories", Frontiers in Psychology, 7/8/2013.
- Mike Wood, "What does online discussion tell us about the psychology of conspiracy theories?", The Psychology of Conspiracy Theories, 7/10/2013.
- Mike Wood, "Setting the record straight on Wood & Douglas, 2013", The Psychology of Conspiracy Theories, 7/13/2013.
- Mike Wood, "The Wood & Douglas (2013) commission report: Whitewash or coverup?", The Psychology of Conspiracy Theories, 7/28/2013.
Fallacy: Unrepresentative Sample
Update (12/20/2016): I've edited this entry to make the abbreviations consistent.
December 13th, 2016 (Revised: 7/5/2024) (Permalink)
Lesson in Logic 15: Contradiction
In the previous lesson, you learned how to use Venn diagrams to tell whether or not two categorical statements are logically equivalent. In this lesson, you'll learn how to use the diagrams to tell whether two such sentences contradict one another.
As explained in the previous lesson, logically equivalent statements are ones that say the same thing, logically. Contradictory statements are ones that say the "opposite", logically. A more precise way of putting this is that contradictory statements must have opposite truth-values, that is, if one is true then the other is false, and vice versa.
An important fact about logical equivalence is that there isn't just one statement that is logically equivalent to a given statement, but many―in fact, infinitely many, though I won't bother proving so here; just think about it. Similarly, there are many statements―again, infinitely many―that contradict a given statement, all of which are logically equivalent to each other.
Whereas Venn diagrams of logically equivalent statements are either identical or mirror images of each other, diagrams of contradictory statements are like the negative and positive images of a black-and-white photograph. A negative has black where the positive image has white, and white where the positive image has black. Similarly, a Venn diagram of a statement has shading where the diagram of a contradiction has an X, and Xs where the contradictory diagram has shading.
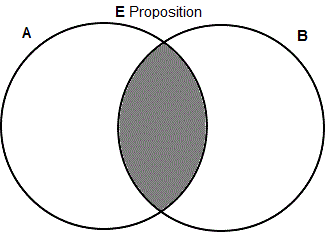
For example, consider the statement: No cats are pets. First off, draw a Venn diagram of this statement. Since this is an E statement, the diagram will be the typical one in which the central, overlap region is shaded. If we let A=cats and B=pets, then the generic E statement diagram to the right represents the example.
As explained above, a contradictory diagram will shade those regions that the diagram of the contradicted statement has Xs―in this case, there are no Xs in the diagram. However, it will also have Xs in those regions of the contradicted diagram that have shading. Since the diagram in this example has shading in the (American) football-shaped region, the contradictory diagram will have an X in that region―see the diagram below and to the right.

Now, if you've been following along carefully in these lessons, you will recognize the resulting diagram as the typical one for an I statement. Thus, the categorical I statement "some cats are pets" contradicts "no cats are pets". Intuitively, this should seem correct, since if one of these two statements is true then the other will be false, and vice versa, which is the definition of contradiction.
So, if you wish to tell whether two categorical statements are contradictory, draw Venn diagrams for each statement labelling the circles the same way in each diagram. If the diagram of each statement is a negative image of the other―that is, has Xs where the other has shading and shading where the other has Xs―then the statements are contradictories; if not, not.
Assuming that you are familiar enough with Venn diagrams to read off a categorical statement from a diagram, you can also use a Venn diagram to discover a contradiction of a given statement. Just draw a Venn diagram of the statement that you wish to contradict, produce its negative image, then read off a contradictory statement from the diagram. Give it a try in the exercises below.
Exercises:
- What is a contradiction of "some cats are not pets"?
There are, of course, infinitely many, but one is: "All cats are pets." If you came up with a different answer, that's okay as long as it is logically equivalent to "all cats are pets."
- Does "some pets are cats" contradict "some cats are not pets"?
No, "some pets are cats" says the same thing as "some cats are pets", by conversion―that is, they are equivalent; see previous lesson―and both sentences are true, so they can't contradict each other.
- Do "no non-mammals are bats" and "some bats are non-mammals" contradict one another?
Yes. "No non-mammals are bats" is logically equivalent to "no bats are non-mammals", by conversion, which is logically equivalent to "all bats are mammals", by obversion. "Some bats are non-mammals" is obviously equivalent to "some bats are not mammals", which contradicts "all bats are mammals".
- What is a contradiction of "all cats are non-pets"?
Again, there are infinitely many. As you may remember from the previous lesson, "all cats are non-pets" is logically equivalent to "no cats are pets", so "some cats are pets" contradicts it. If you got a different answer, it should be logically equivalent to "some cats are pets".
- Are "all cats are pets" and "no pets are cats" contradictory?
No, both of these statements are false: since some cats are feral, and so not pets, it's not true that all cats are pets. "No pets are cats" is false because some people have pet cats. So, the two statements are not contradictories.
Previous Lessons:
- Lesson in Logic 11: Class Diagrams, 6/22/2016
- Lesson in Logic 12: Two-Circle Venn Diagrams, 7/16/2016
- Lesson in Logic 13: Categorical Statements, 8/17/2016
- Lesson in Logic 14: Equivalence, 11/15/2016