Previous Month | RSS/XML | Current | Next Month

WEBLOG

April 28th, 2017 (Permalink)

Lesson in Logic 17: Pretzel Logic

"So, other than solving puzzles1, what is a three-circle Venn diagram2 good for?", you may ask. I'm glad you asked that question!

In previous lessons, you learned how to use the two-circle Venn diagram to tell when two categorical statements are logically equivalent3 and contradictory4. In the next lesson, you'll discover how to use the three-circle diagram―or "pretzel"5―to test categorical syllogisms for validity. This one is preparatory for the next; in this one, you'll learn how to diagram categorical statements onto a pretzel.

If you remember from a previous lesson6 how to diagram the four types of categorical statement onto a two-circle diagram, then doing so on a three-circle one should be fairly easy7. It's mostly a matter of concentrating on the two relevant circles and ignoring the third. However, there are some subtleties that you need to learn, especially involving the I and O statements, or you'll end up making mistakes. It's those subtleties that you should learn from this lesson, as well as getting some practice at diagramming on three circles. 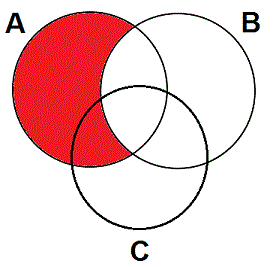All As are Bs.

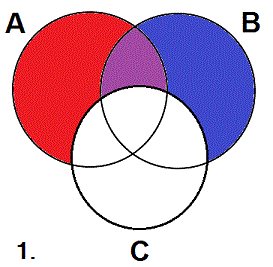
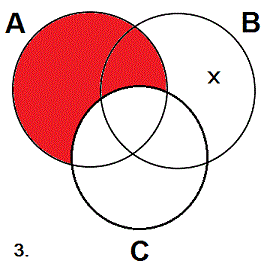
As you should remember, the four types of categorical statement, A, E, I, and O, relate two class terms. A categorical syllogism contains three such statements with a total of three class terms, which is why it can be diagrammed on a three-circle diagram, with each circle representing one of the three classes. However, each statement only has two class terms, so when you diagram it on the three circles you should pretend that the third circle8 does not exist. For example, suppose that you wish to diagram the A statement "All As are Bs" on a pretzel with classes A, B, and C. Simply ignore the C-circle and diagram the statement on the two circles as shown in red. 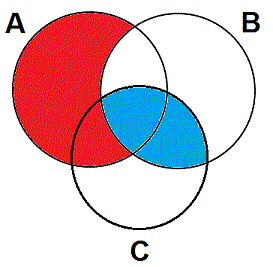No Bs are Cs.

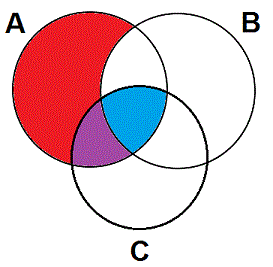
Similarly, if you want to diagram the E statement "No Bs are Cs" on the same diagram you should ignore the A circle, as shown in blue. We've now diagrammed two categorical statements―"All As are Bs" and "No Bs are Cs"―on a single pretzel, which is what you need to do to diagram a syllogism. So far, this should be easy as long as you remember how to diagram the A and E statements. All As are Bs and no Cs are As.

A slight complication arises if the areas that you need to shade when diagramming the two statements overlap. For instance, supposing you wish to diagram both "All As are Bs" and "No Cs are As" on a single pretzel. Diagramming just "All As are Bs" will, of course, produce the first diagram above. However, diagramming "No Cs are As" on the same diagram will involve shading the same area twice, as shown in purple. The purple area is shaded by both the red and blue shading, hence its color.

Now, remember that shading an area just means that the area is empty. So, it's not necessary to use different colors to mark an area as shaded twice, since a doubly-shaded area is not doubly empty. I just do that to show the area of overlap, and because it's pretty.

That's all there is to diagramming A and E statements, but Is and Os are tricky. Unfortunately, you cannot simply ignore the third circle when diagramming an I or O statement. For example, suppose that you want to diagram "Some As are Bs" on a pretzel. To do so, you need to place an X in the area of overlap of the two circles for A and B. However, that area is now divided in two by the circle for C. Where should you put the X: above or below the curve of the C circle that divides the overlap area in two?

Remember what the X represents: it tells us that the area it occupies is non-empty, that is, that there is something in that area. For this reason, you cannot simply place it in either of the two sub-areas of the overlap region. If you put it in the area inside the C circle, that would mean that some As that are also Cs are Bs; whereas, if you put it in the area outside the C circle, that would mean that some As that are not Cs are Bs. Moreover, if you put two Xs in the overlap area, one in each sub-area, that would mean that there are at least two As that are Bs, one of which is also C and one that is not. However, all that the I statement says is that some As are Bs; it does not say whether or not they are also Cs.

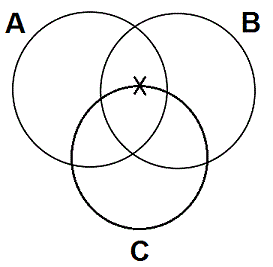
For this reason, you need to learn two new diagramming conventions for I and O statements: Some As are Bs.

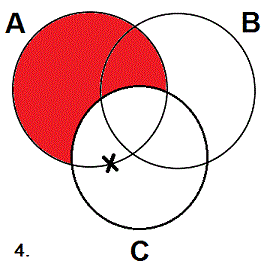
  1. When you need to place an X in an area of the diagram that is divided into two sub-areas, place the X on the line dividing the area in two. So, the way to diagram the I statement "Some As are Bs" on the three circles is as shown.
  2. When diagramming two categorical statements on a pretzel, one of which is an A or E and the other is an I or O, always diagram the A or E statement first. In other words, always shade before Xing.

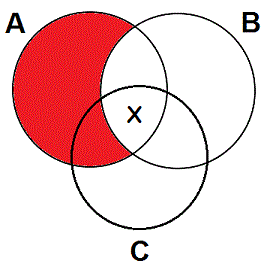
All As are Bs and some Cs are As.

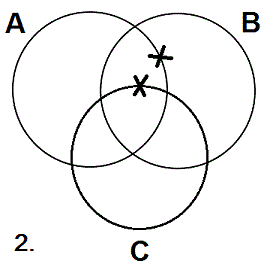
The reason for the second convention can best be seen via an example: Suppose that you want to diagram both "All As are Bs" and "Some Cs are As" at the same time. If you diagram the A statement first, you'll get the first diagram above. Now, when you want to diagram the I statement, you will be forced to put it into the central overlap section, as shown.

The reason you put the "X" in the central overlap is because you know from the A statement that the area representing As that are Cs but not Bs is empty. Xs and shading are like matter and anti-matter: they don't go together. If you put an X in a shaded area, that would say that the area was empty but had something in it, which is contradictory. Moreover, you shouldn't put an "X" on a line between a shaded area and an unshaded one, since the shaded area is empty and the object that the "X" represents must be in the unshaded area.

So, when diagramming two categorical statements on a pretzel, do the following:

  1. Diagram A and E statements;
  2. Do so by ignoring the third circle8;
  3. Diagram I and O statements;
  4. If you must place an "X" in an area divided into two sub-areas, place it on the dividing line between the sub-areas.

That's it! Now you're ready to start diagramming categorical syllogisms, which you will learn how to evaluate in the next lesson. Check whether you're ready for it with the exercises below.

Exercises: Diagram the following pairs of statements on a pretzel.

  1. All As are Cs; all Bs are Cs.
  2. Some As are Bs; some Bs are not Cs.
  3. All As are Cs; some Bs are not Cs.
  4. All As are Cs; some Cs are not Bs.

Answers to the Exercises

Next Lesson: Learn how to use pretzels to test the validity of categorical syllogisms.

Notes:

  1. Using Venn Diagrams to Solve Puzzles, Part 2, 3/7/2017
  2. Lesson in Logic 16: The Third Circle, 2/16/2017
  3. Lesson in Logic 14: Equivalence, 11/15/2016
  4. Lesson in Logic 15: Contradiction, 12/13/2016
  5. I call the three-circle Venn diagram a "pretzel" because it looks a little bit like one, and because "pretzel" is shorter.
  6. Lesson in Logic 13: Categorical Statements, 8/17/2016
  7. If you don't remember, you'd better go back and review.
  8. That is, the one not related by the two class terms of the statement.
April 22nd, 2017 (Permalink)

The ABC Murder

Detective David Davidson was assigned to investigate the murder of notorious racketeer Victor Timm. It should have been an open-and-shut case since there were four eyewitnesses to the crime. Unfortunately for Davidson, the witnesses all disagreed.

The ABC Gang was so called because it consisted of three criminals: Adam Adamson, Brad Bradford, and Curt Curtis. It was known that the ABC Gang and Timm had had a falling out, but who was the triggerman? He had no doubt that the shooter was one of the ABC gangsters, but which one?

Davidson set up a line-up for the witnesses that included all three of the ABC gangmembers, together with a few fellow cops as ringers. Thankfully, none of the witnesses fingered any of the cops as the killer. Here's the gist of what each witness said:

  1. Adamson was the shooter.
  2. This witness wouldn't identify a shooter, but insisted that it wasn't Curtis.
  3. This one wasn't sure whether Adamson or Bradford was the shooter, but claimed that it was one of the two.
  4. The last witness refused to finger the shooter as Bradford but did rule out both Adamson and Curtis.

Davidson was disgusted. That didn't help at all! In fact, at least one of the witnesses had to be wrong since they contradicted each other. Luckily, Davidson received a call from a stoolie named Eddie "The Snitch" Edwards who informed him that one or more of the witnesses had been bribed or intimidated by the ABC Gang to lie to the police. At first, Davidson was still disgusted, since he already knew that at least one of the witnesses had not told the truth, but he didn't know which. However, when Eddie told him the exact number of witnesses who weren't telling the truth, Davidson smiled. Davidson now knew who the shooter was.

Assuming that one of the ABC gangsters was the shooter and that Eddie's information was correct, who shot Vic Timm?

Solution

April 9th, 2016 (Permalink)

Check it Out, Too

If you can tear yourself away from the tax forms long enough, philosopher Alan Hájek offers you a "philosophy tool kit" for thinking:

Philosophers pride themselves on thinking clearly by seeing what follows from what, exposing sophisms, spotting fallacies, and generally policing our reasoning. … But these skills are not the exclusive property of rarefied sages, accessed only with a secret handshake and insider training, as much as some philosophers wish this were so. Instead, some of these skills can be captured by generalisable, all-purpose techniques for the proper conduct of thought, whatever the topic. Many of these are easily taught and learned. As such, they can be utilised by non-philosophers too. At a time when we are bombarded more than ever with specious claims and spurious inferences, clear thinking provides a much-needed safeguard that we should all strive towards.1

It's not a full philosophical "tool kit", as it contains only a few tools. Rather, it's like the kind of small kit you might keep in your car in case of a breakdown on the road, so you might think of it as a tool kit in case of a philosophical emergency.

Hájek shows how to use the tools by applying them to some traditional philosophical problems but, as he mentions, they can be applied to many other types of intellectual, conceptual, and logical problems.

The tools in the kit are philosophical heuristics, but what is a philosophical heuristic? Well, wait: what is a heuristic? It's a rule of thumb2. Hájek gives the following example: "Here’s a good one for mathematics: if you are not making headway on a problem, modify it slightly to make it easier, and solve that one." I think this is a good rule of thumb for problem-solving in general, not just mathematics. The point of using heuristics is that, while they don't always work, they work often enough to be useful; also, even when they don't solve the problem, they may help point the way to a solution.

One reason I point you to this article is that many of the topics that Hájek discusses have been discussed here in The Fallacy Files, so you can compare his treatment of the issues to mine3:

This should keep you busy until I can get around to posting something new.

Notes:

  1. Alan Hájek, "Philosophy Tool Kit", Aeon, 4/3/2017
  2. And, no, the phrase "rule of thumb" does not come from a law allowing a man to beat his wife with any stick no thicker than his thumb. See: Cecil Adams, "Does 'rule of thumb' refer to an old law permitting wife beating?", The Straight Dope, 5/12/2000
  3. A useful tool that Hájek doesn't mention is "the second opinion".
  4. "A" v. "The", 7/19/2008
  5. "False Dichotomy"
  6. Puzzle it Out, 7/3/2015
  7. Q&A, 5/21/2013
  8. The Logical Problem of Evil, 4/6/2015
April 5th, 2017 (Permalink)

Check it Out

April is the cruelest month….1

…And April 15th the cruelest day. It's that time of year again, and I'm going to be rather busy for the next couple of weeks trying to figure out what the IRS wants from me. In the meantime, if you can find some time to read something other than tax instructions, here's something worth checking out2.

Notes:

  1. T. S. Eliot, "The Waste Land", Poetry Foundation
  2. Eugene Volokh, "“Amid ‘Trump Effect’ fear, 40% of colleges see dip in foreign applicants”―but…", The Volokh Conspiracy, 3/28/2017

Solution to the ABC Murder: Curt Curtis (no relation) was the shooter.

In case you got the wrong answer, here's how to solve this puzzle: We know that at least one of the witnesses is not telling the truth, since the first witness accused Adamson but the last one claimed that Adamson was not the shooter. However, it may be that one or more of the other witnesses is not telling the truth.

Given that one of the ABC gang shot Timm, there are only three possible shooters to consider:

  1. Adamson: In this case, only the last witness did not tell the truth, since he or she claimed that Adamson was not the shooter.
  2. Bradford: Only the first witness did not tell the truth, since he or she claimed that Adamson was the shooter.
  3. Curtis: In this case, all four of the witnesses would have failed to tell the truth, since the identifications made by each are inconsistent with Curtis being the shooter.

When Eddie the Snitch informed Detective Davidson that at least one of the witnesses was not telling the truth, this fact did not help Davidson since that meant that each of the three gangsters might have been the shooter. However, when Eddie went on to tell Davidson the exact number of witnesses who were not telling the truth, Davidson was able to solve the case. How was he able to do so?

If Eddie had said that only one of the witnesses was not telling the truth, then all this would have done is rule out Curtis as the shooter. If Eddie had said that two or three of the witnesses were not telling the truth, then Davidson would have concluded that Eddie was the one who was wrong. The only way in which Eddie's information would have helped Davidson solve the case is if Eddie had said that all four of the witnesses were not telling the truth. Therefore, Curtis was the shooter.

Disclosure: The story you have just read is false. The names have been changed to protect the guilty.

Answers to the Exercises:

All As are Cs; all Bs are Cs. Some As are Bs; some Bs are not Cs. All As are Cs; some Bs are not Cs. All As are Cs; some Cs are not Bs.

Previous Month | RSS/XML | Current | Next Month